Compact Letter Display (CLD)
What is it?
Compact letter displays are often used to report results of all pairwise comparisons among treatment means in comparative experiments. See Piepho (2004) and Piepho (2018) for more details and find a coding example below.
| Group | Mean weight* |
|---|---|
| Trt1 | 4.7\(^{a}\) |
| Ctrl | 5.0\(^{ab}\) |
| Trt2 | 5.5\(^{b}\) |
How to
get the letters
You will need to install the packages emmeans, multcomp and {multcompView}. The example given here is based on the PlantGrowth data, which is included in R.
library(emmeans)
library(multcomp)
library(multcompView)
# set up model
model <- lm(weight ~ group, data = PlantGrowth)
# get (adjusted) weight means per group
model_means <- emmeans(object = model,
specs = "group")
# add letters to each mean
model_means_cld <- cld(object = model_means,
adjust = "Tukey",
Letters = letters,
alpha = 0.05)
# show output
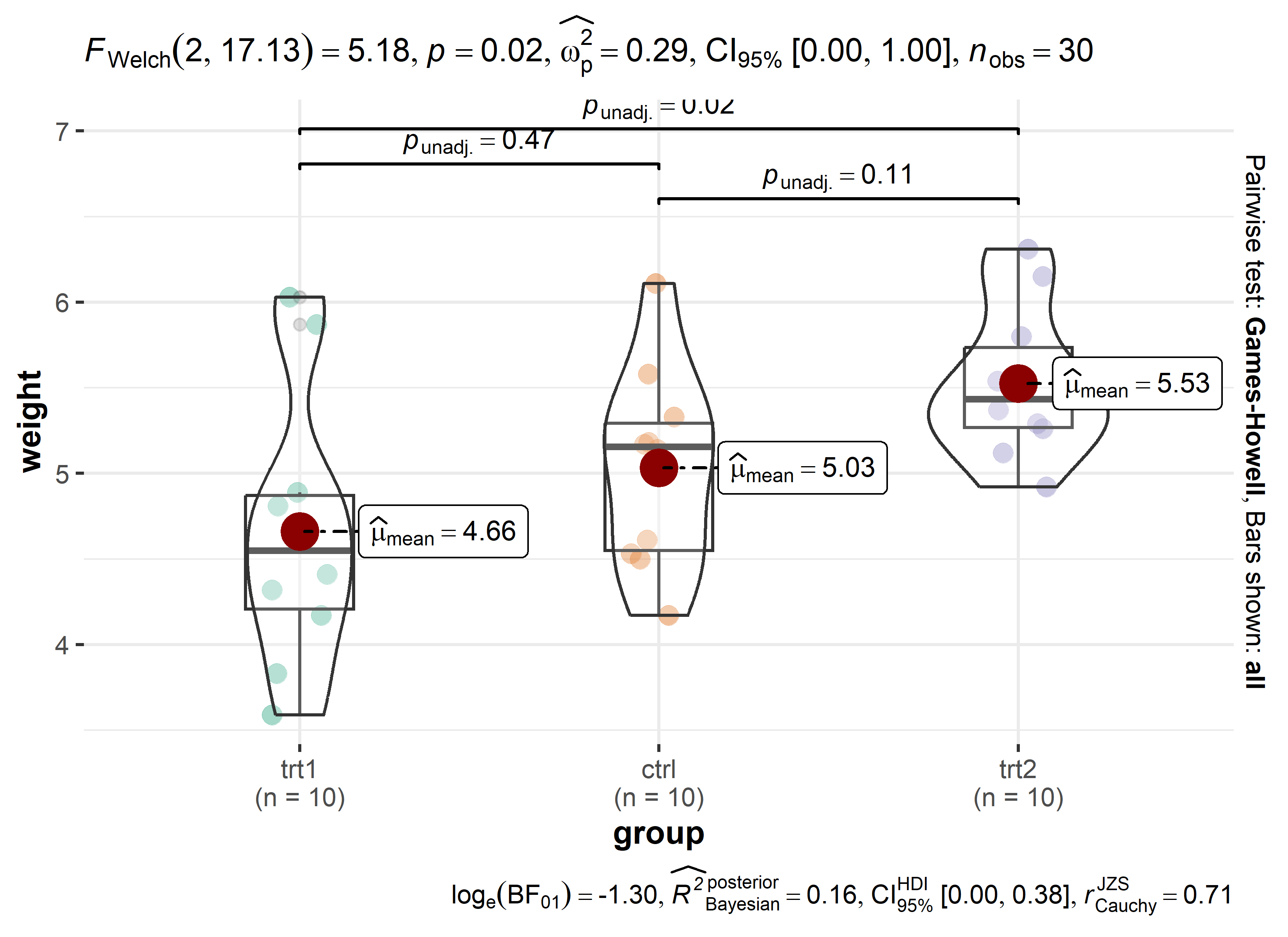
model_means_cld group emmean SE df lower.CL upper.CL .group
trt1 4.66 0.197 27 4.16 5.16 a
ctrl 5.03 0.197 27 4.53 5.53 ab
trt2 5.53 0.197 27 5.02 6.03 b
Confidence level used: 0.95
Conf-level adjustment: sidak method for 3 estimates
P value adjustment: tukey method for comparing a family of 3 estimates
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. -
We set up a model
- This is a very simple example using
lm(). You may use much more complex models and many other model classes.
- This is a very simple example using
-
emmeans()estimates adjusted means per group.-
specs =lets you define for which factor levels you want the means - Note that when doing this for mixed models, one should use the Kenward-Roger method adjusting the denominator degrees of freedom. One may add the
lmer.df = "kenward-roger"argument, yet this is the default in {emmeans} (Details here)! Also note that you cannot go wrong with this adjustment - even if there is nothing to adjust.
-
-
cld()adds the letters in a new column named.group.-
adjust =lets you choose the p-value adjustment method. It allows for different multiplicity adjustments. Go to the “P-value adjustments” heading within the “summary.emmGrid” section in the emmeans documentation for more details on e.g. Fisher’s LSD test, Tukey-test, Bonferroni adjustment etc. -
Letters = lettersis needed because for some reason the default are numbers and not letters… even though the function is called Compact Letter Display?! -
alpha =lets you choose the significance level for the comparisons.
-
If you get the following note and are irritated by it,
## Note: adjust = "tukey" was changed to "sidak"
## because "tukey" is only appropriate for one set of pairwise comparisons
## Conf-level adjustment: sidak method for 3 estimates.
## P value adjustment: tukey method for comparing a family of 3 estimateshere is an answer explaining why this happens and that it is not a problem. It is not a problem in the sense that the p-values of the pairwise comparisons were indeed adjusted with the Tukey-method, while the Sidak adjustment was applied to the confidence intervals of the means (i.e. columns lower.CL and upper.CL).
interpret the letters
Until August 2022, the note below the cld() outcome would read:
## NOTE: Compact letter displays can be misleading
## because they show NON-findings rather than findings.
## Consider using 'pairs()', 'pwpp()', or 'pwpm()' instead.However, in CRAN version 1.8.0 it was changed to:
## NOTE: If two or more means share the same grouping letter,
## then we cannot show them to be different.
## But we also did not show them to be the same.Both notes are very much in line with the delicate matter of how the CLD must be understood. The author and maintainer of the emmeans package, Russell V. Lenth makes the argument that CLDs convey information in a way that may be misleading to the reader. This is because they “display non-findings rather than findings - they group together means based on NOT being able to show they are different” (personal communication). Furthermore, “[the CLD approach] works, but it is very black-and-white: with alpha = .05, P values slightly above or below .05 make a difference, but there’s no difference between a P value of .051 and one of .987, or between .049 and .00001” (posted here). He even wrote here that “Providing for CLDs at all remains one of my biggest regrets in developing this package”. Finally, the former note suggests using alternative plots, which are also created below.
On the other hand, it must be clear that the information conveyed by CLDs is not wrong as long as it is interpreted correctly. The documentation of the cld() function refers to Piepho (2004), but even more on point in this context is Piepho (2018):
Piepho, Hans-Peter (2018) Letters in Mean Comparisons: What They Do and Don’t Mean, Agronomy Journal, 110(2), 431-434. DOI: 10.2134/agronj2017.10.0580 (ResearchGate)
Abstract
- Letter displays allow efficient reporting of pairwise treatment comparisons.
- It is important to correctly convey the meaning of letters in captions to tables and graphs displaying treatment means.
- The meaning of a letter display can and should be stated in a single sentence without ambiguity.
Letter displays are often used to report results of all pairwise comparisons among treatment means in comparative experiments. In captions to tables and charts using such letter displays, it is crucial to explain properly what the letters mean. In this paper I explain what the letters mean and how this meaning can be succinctly conveyed in a single sentence without ambiguity. This is contrasted to counter-examples commonly found in publications.
Thus, the article (= 4 pages long) is certainly worth a read if you are using CLDs.
get the plots
Here I provide code for two ways of plotting the results via ggplot2. The first plot is the one I would use, while the second plot is one that is traditionally more common. Finally, I provide examples of other plots that I came across that are suggested as alternatives to CLD plots.
plot 1: suggested
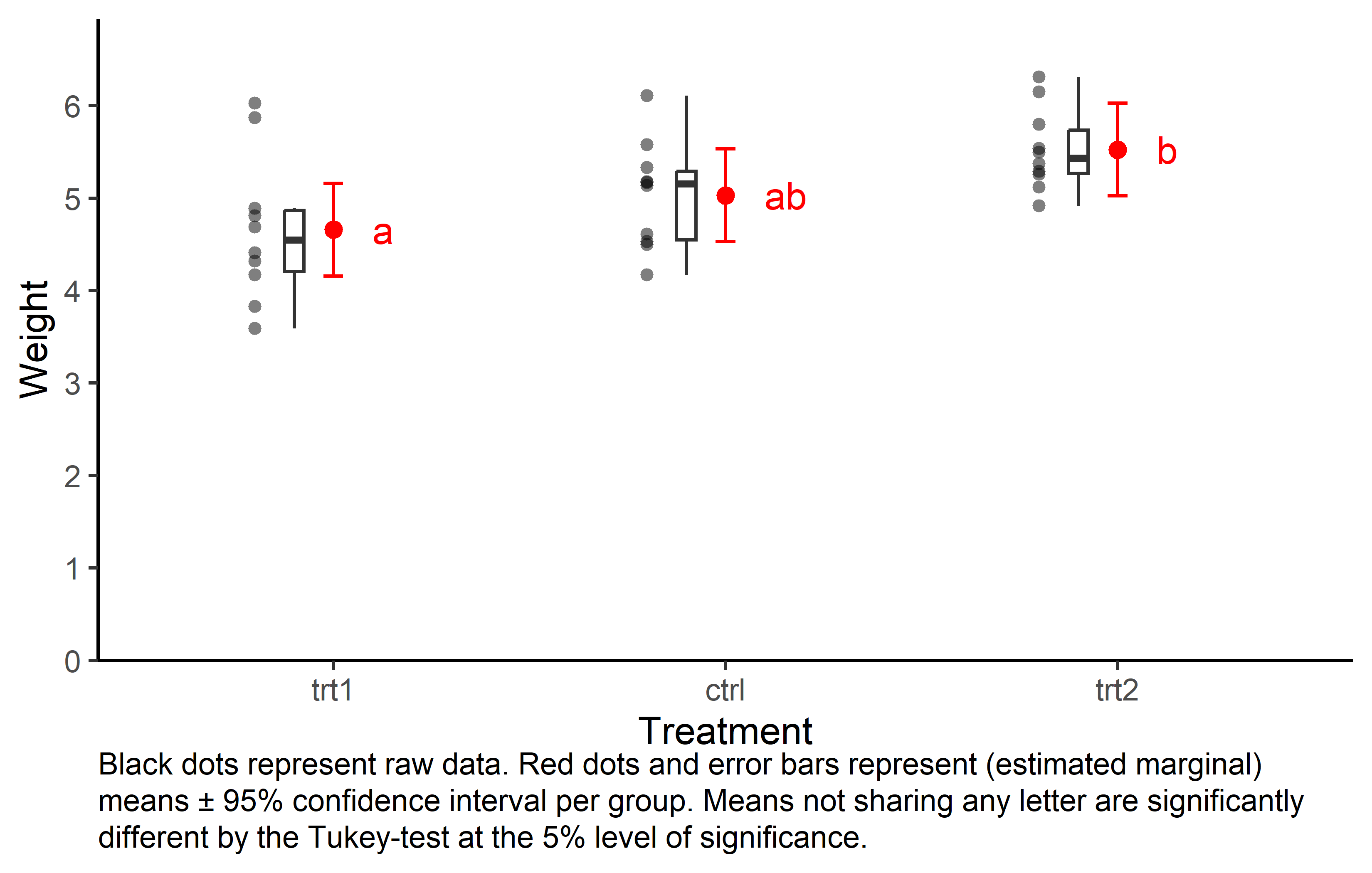
I’ve been using and suggesting to use this type of plot for a while now. I know it contains a lot of information and may seem unfamiliar and overwhelming at first glance. However, I argue that if you take the time to understand what you are looking at, this plot is nice as it shows the raw data (black dots), descriptive statistics (black boxes), estimated means (red dots) and a measure of their precision (red error bars) as well as the compact letter display (red letters).
Code
library(ggtext) # automatic line breaks in caption
library(tidyverse) # ggplot & helper functions
library(scales) # more helper functions
# optional: sort factor levels of groups column according to highest mean
# ...in means table
model_means_cld <- model_means_cld %>%
mutate(group = fct_reorder(group, emmean))
# ...in data table
PlantGrowth <- PlantGrowth %>%
mutate(group = fct_relevel(group, levels(model_means_cld$group)))
# plot
ggplot() +
# y-axis
scale_y_continuous(
name = "Weight",
limits = c(0, NA),
breaks = pretty_breaks(),
expand = expansion(mult = c(0,0.1))
) +
# x-axis
scale_x_discrete(
name = "Treatment"
) +
# general layout
theme_classic() +
theme(plot.caption = element_textbox_simple()) +
# black data points
geom_point(
data = PlantGrowth,
aes(y = weight, x = group),
shape = 16,
alpha = 0.5,
position = position_nudge(x = -0.2)
) +
# black boxplot
geom_boxplot(
data = PlantGrowth,
aes(y = weight, x = group),
width = 0.05,
outlier.shape = NA,
position = position_nudge(x = -0.1)
) +
# red mean value
geom_point(
data = model_means_cld,
aes(y = emmean, x = group),
size = 2,
color = "red"
) +
# red mean errorbar
geom_errorbar(
data = model_means_cld,
aes(ymin = lower.CL, ymax = upper.CL, x = group),
width = 0.05,
color = "red"
) +
# red letters
geom_text(
data = model_means_cld,
aes(
y = emmean,
x = group,
label = str_trim(.group)
),
position = position_nudge(x = 0.1),
hjust = 0,
color = "red"
) +
# caption
labs(
caption = "Black dots represent raw data. Red dots and error bars represent (estimated marginal) means ± 95% confidence interval per group. Means not sharing any letter are significantly different by the Tukey-test at the 5% level of significance."
)plot 2: well-known
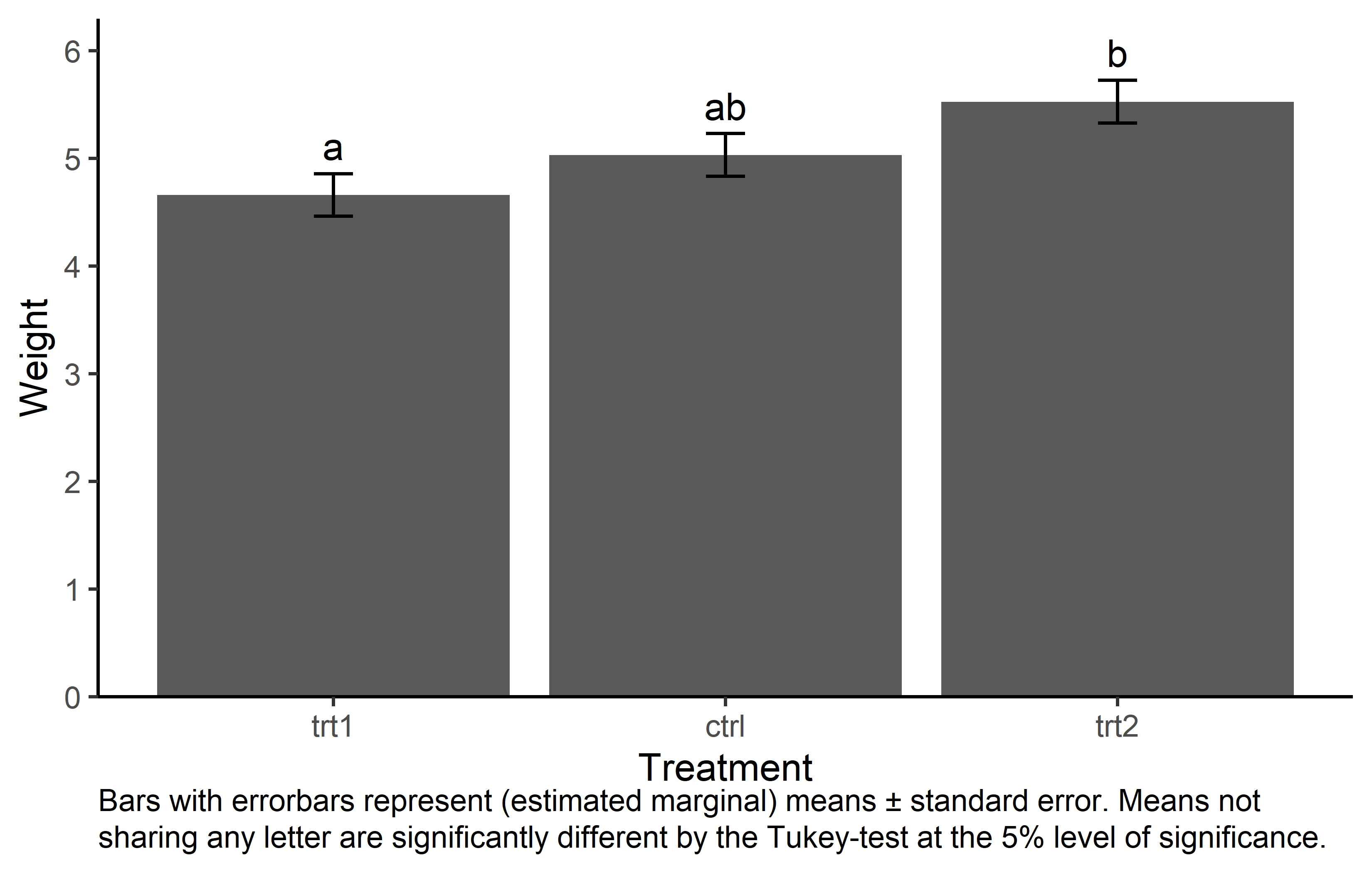
Traditionally, bar plots with error bars are used a lot in this context. In my experience, there is at least one poster with one of them in every university building I. While they are not wrong per se, there is a decade-long discussion about why such “dynamite plots” are not optimal (see e.g. this nice blogpost).
Code
library(ggtext) # automatic line breaks in caption
library(tidyverse) # ggplot & helper functions
library(scales) # more helper functions
# optional: sort factor levels of groups column according to highest mean
# ...in means table
model_means_cld <- model_means_cld %>%
mutate(group = fct_reorder(group, emmean))
# ...in data table
PlantGrowth <- PlantGrowth %>%
mutate(group = fct_relevel(group, levels(model_means_cld$group)))
# plot
ggplot() +
# y-axis
scale_y_continuous(
name = "Weight",
limits = c(0, NA),
breaks = pretty_breaks(),
expand = expansion(mult = c(0,0.1))
) +
# x-axis
scale_x_discrete(
name = "Treatment"
) +
# general layout
theme_classic() +
theme(plot.caption = element_textbox_simple()) +
# bars
geom_bar(data = model_means_cld,
aes(y = emmean, x = group),
stat = "identity") +
# errorbars
geom_errorbar(data = model_means_cld,
aes(
ymin = emmean - SE,
ymax = emmean + SE,
x = group
),
width = 0.1) +
# letters
geom_text(
data = model_means_cld,
aes(
y = emmean + SE,
x = group,
label = str_trim(.group)
),
hjust = 0.5,
vjust = -0.5
) +
# caption
labs(
caption = "Bars with errorbars represent (estimated marginal) means ± standard error. Means not sharing any letter are significantly different by the Tukey-test at the 5% level of significance."
)alternative plots
Note that I simply collect alternative ways of plotting adjusted mean comparisons here - this does not mean I fully grasp their concept.
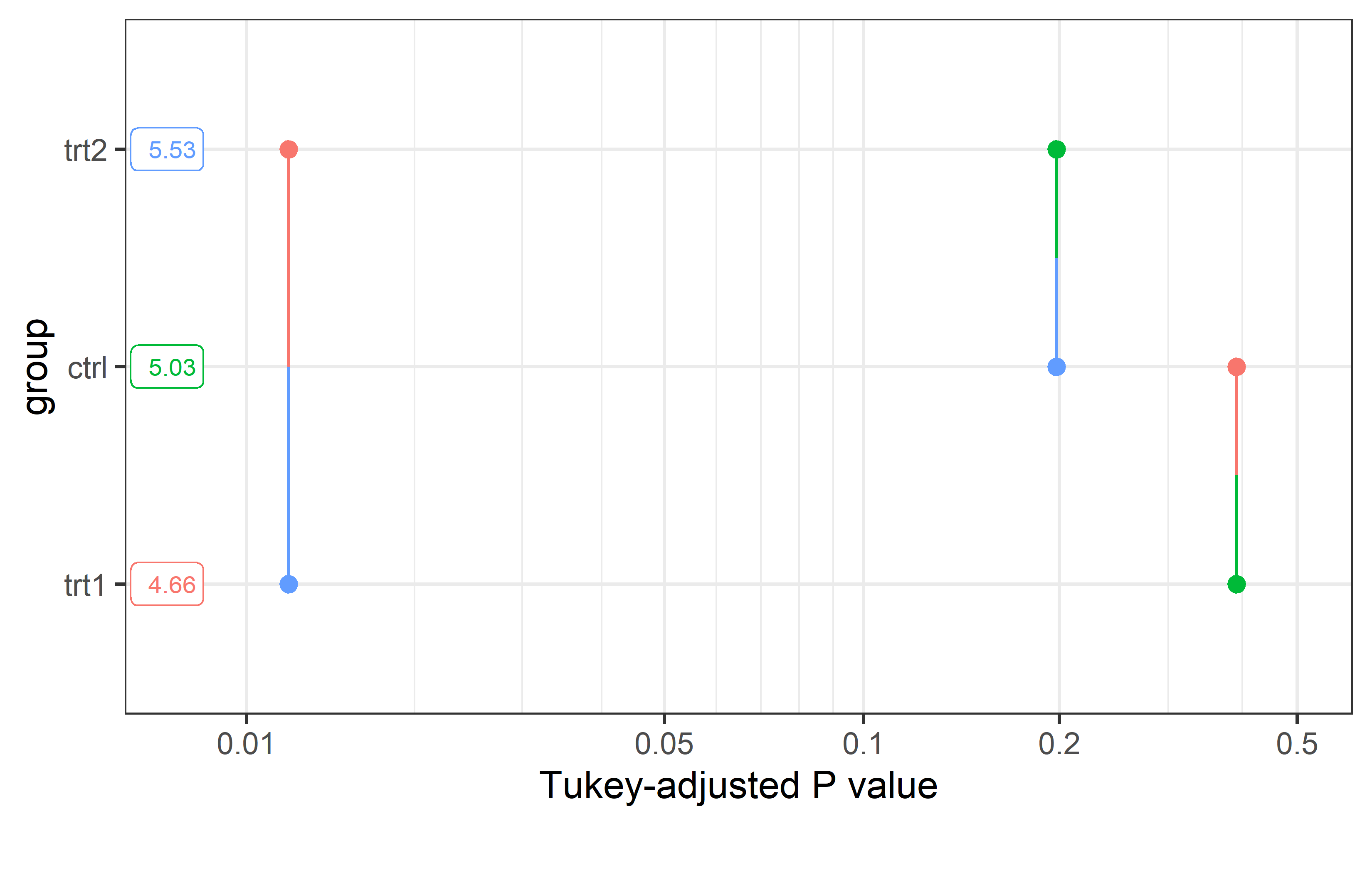
alt 1: Pairwise P-value plot {emmeans}
This is the Pairwise P-value plot suggested in the former NOTE we received above as an alternative. The documentation reads: Factor levels (or combinations thereof) are plotted on the vertical scale, and P values are plotted on the horizontal scale. Each P value is plotted twice – at vertical positions corresponding to the levels being compared – and connected by a line segment. Thus, it is easy to visualize which P values are small and large, and which levels are compared.
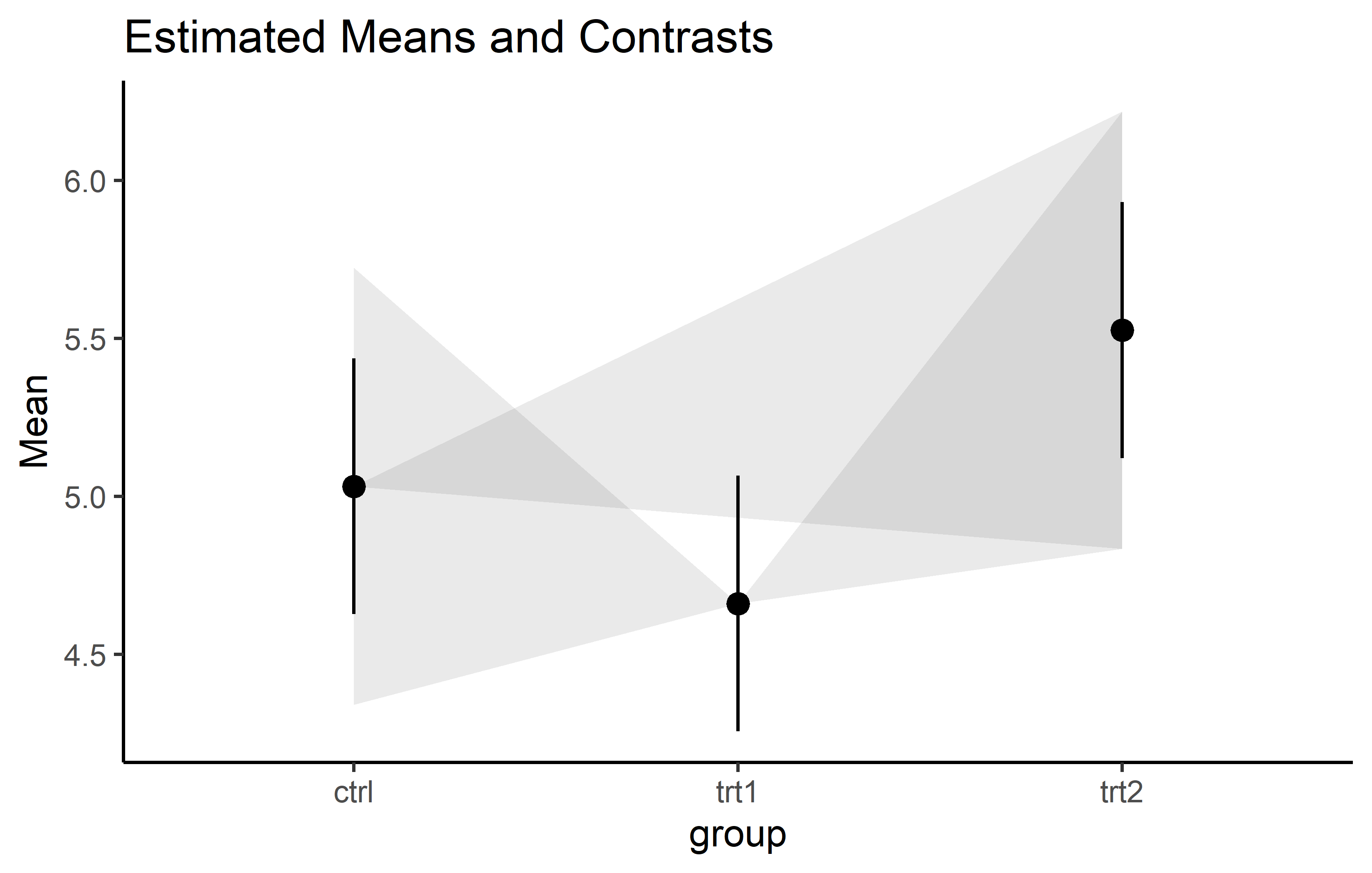
alt 2: Lighthouse plot {easystats}
Within the framework of the easystats packages, the lighthouse plots came up as a more recent idea. See this issue and this and this part of the documentation for more details.
Code
library(modelbased)
library(see)
plot(estimate_contrasts(model, adjust = "tukey"),
estimate_means(model)) +
theme_classic()alt 3: The {ggbetweenstats} plot
Finally, the ggstatsplot package’s function ggbetweenstats() aims to create graphics with details from statistical tests included in the information-rich plots themselves and would compare our groups like this:
Code
library(PMCMRplus)
library(rstantools)
library(ggstatsplot)
# "since the confidence intervals for the effect sizes are computed using
# bootstrapping, important to set a seed for reproducibility"
set.seed(42)
ggstatsplot::ggbetweenstats(
data = PlantGrowth,
x = group,
y = weight,
pairwise.comparisons = TRUE,
pairwise.display = "all",
p.adjust.method = "none"
)see the comparisons
The compact letter display allows us to understand the statistical significances forall pairwise comparisons without ever having to look at the individual comparisons a.k.a. contrasts. Yet, if you do want to look at them, here are two options that both start with the model_means object we created at the beginning of this document.
We can simply use details = TRUE in the cld() function. This adds a second table called comparisons to the output.
$emmeans
group emmean SE df lower.CL upper.CL .group
trt1 4.66 0.197 27 4.26 5.07 a
ctrl 5.03 0.197 27 4.63 5.44 ab
trt2 5.53 0.197 27 5.12 5.93 b
Confidence level used: 0.95
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same.
$comparisons
contrast estimate SE df t.ratio p.value
ctrl - trt1 0.371 0.279 27 1.331 0.1944
trt2 - trt1 0.865 0.279 27 3.103 0.0045
trt2 - ctrl 0.494 0.279 27 1.772 0.0877However, we do not actually nee multcomp::cld() function if we only want to investigate the individual pairwise comparisons. Moreover, when using emmeans::pairs() on the means object that we created via emmeans::emmeans(), we can set infer = c(TRUE, TRUE) to obtain both the confidence interval1 and p-values for each difference.
contrast estimate SE df lower.CL upper.CL t.ratio p.value
ctrl - trt1 0.371 0.279 27 -0.201 0.943 1.331 0.1944
ctrl - trt2 -0.494 0.279 27 -1.066 0.078 -1.772 0.0877
trt1 - trt2 -0.865 0.279 27 -1.437 -0.293 -3.103 0.0045
Confidence level used: 0.95 get the LSD/HSD
The least significant difference (LSD) represents the smallest value a difference between two means would need to be in order to be statistically significant according to the Fisher’s LSD test (i.e. have a p-value < 0.05). In a simple setting (i.e. balanced data and standard confidence interval), the LSD is simply the half-width of the confidence interval and for our example 0.572:
model_means %>%
pairs(adjust = "none",
infer = c(TRUE, TRUE)) %>%
as_tibble() %>%
mutate(LSD = upper.CL - estimate)# A tibble: 3 × 9
contrast estimate SE df lower.CL upper.CL t.ratio p.value LSD
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 ctrl - trt1 0.371 0.279 27 -0.201 0.943 1.33 0.194 0.572
2 ctrl - trt2 -0.494 0.279 27 -1.07 0.0780 -1.77 0.0877 0.572
3 trt1 - trt2 -0.865 0.279 27 -1.44 -0.293 -3.10 0.00446 0.572The honestly significant difference (HSD) is basically the Tukey-version of the LSD and for our example 0.691:
model_means %>%
pairs(adjust = "Tukey",
infer = c(TRUE, TRUE)) %>%
as_tibble() %>%
mutate(HSD = upper.CL - estimate)# A tibble: 3 × 9
contrast estimate SE df lower.CL upper.CL t.ratio p.value HSD
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 ctrl - trt1 0.371 0.279 27 -0.320 1.06 1.33 0.391 0.691
2 ctrl - trt2 -0.494 0.279 27 -1.19 0.197 -1.77 0.198 0.691
3 trt1 - trt2 -0.865 0.279 27 -1.56 -0.174 -3.10 0.0120 0.691Note that the LSD or HSD is not necessarily a single value for all comparisons as e.g. shown here. This was actually the core point of (all publications in) my PhD (full text on ResearchGate): Modern experiments do not always lead to balanced/orthogonal data and simple variance structures. However, only if both of these conditions are given, the LSD/HSD will be a single constant value across all comparisons.
get the mean standard error of differences
It is sometimes useful to extract the average/mean standard error of differences (s.e.d.)2. Here is an efficient way of obtaining it:
deal with significant interactions
For now, please check out my answer here on stackoverflow.
References
Footnotes
Citation
@online{schmidt2023,
author = {Paul Schmidt},
title = {Compact {Letter} {Display} {(CLD)}},
date = {2023-06-17},
url = {https://schmidtpaul.github.io/dsfair_quarto//ch/summaryarticles/compactletterdisplay.html},
langid = {en}
}