One-way randomized complete block design
Data
This example is taken from Chapter “2 Randomized complete block design” of the course material “Mixed models for metric data (3402-451)” by Prof. Dr. Hans-Peter Piepho. It considers data published in Clewer and Scarisbrick (2001) from a yield (t/ha) trial laid out as a randomized complete block design (3 blocks) with cultivar (4 cultivars) being the only treatment factor. Thus, we have a total of 12 plots.
Import
# data is available online:
path <- "https://raw.githubusercontent.com/SchmidtPaul/dsfair_quarto/master/data/Clewer&Scarisbrick2001.csv"dat <- read_csv(path) # use path from above
dat# A tibble: 12 × 5
block cultivar yield row col
<chr> <chr> <dbl> <dbl> <dbl>
1 B1 C1 7.4 2 1
2 B1 C2 9.8 3 1
3 B1 C3 7.3 1 1
4 B1 C4 9.5 4 1
5 B2 C1 6.5 1 2
6 B2 C2 6.8 4 2
7 B2 C3 6.1 3 2
8 B2 C4 8 2 2
9 B3 C1 5.6 2 3
10 B3 C2 6.2 1 3
11 B3 C3 6.4 3 3
12 B3 C4 7.4 4 3Format
Before anything, the columns block and cultivar should be encoded as factors, since R by default encoded them as character.
Explore
We make use of dlookr::describe() to conveniently obtain descriptive summary tables. Here, we get can summarize per block and per cultivar.
dat %>%
group_by(cultivar) %>%
dlookr::describe(yield) %>%
select(2:sd) %>%
arrange(desc(mean))# A tibble: 4 × 5
cultivar n na mean sd
<fct> <int> <int> <dbl> <dbl>
1 C4 3 0 8.3 1.08
2 C2 3 0 7.6 1.93
3 C3 3 0 6.6 0.624
4 C1 3 0 6.5 0.9 dat %>%
group_by(block) %>%
dlookr::describe(yield) %>%
select(2:sd) %>%
arrange(desc(mean))# A tibble: 3 × 5
block n na mean sd
<fct> <int> <int> <dbl> <dbl>
1 B1 4 0 8.5 1.33
2 B2 4 0 6.85 0.819
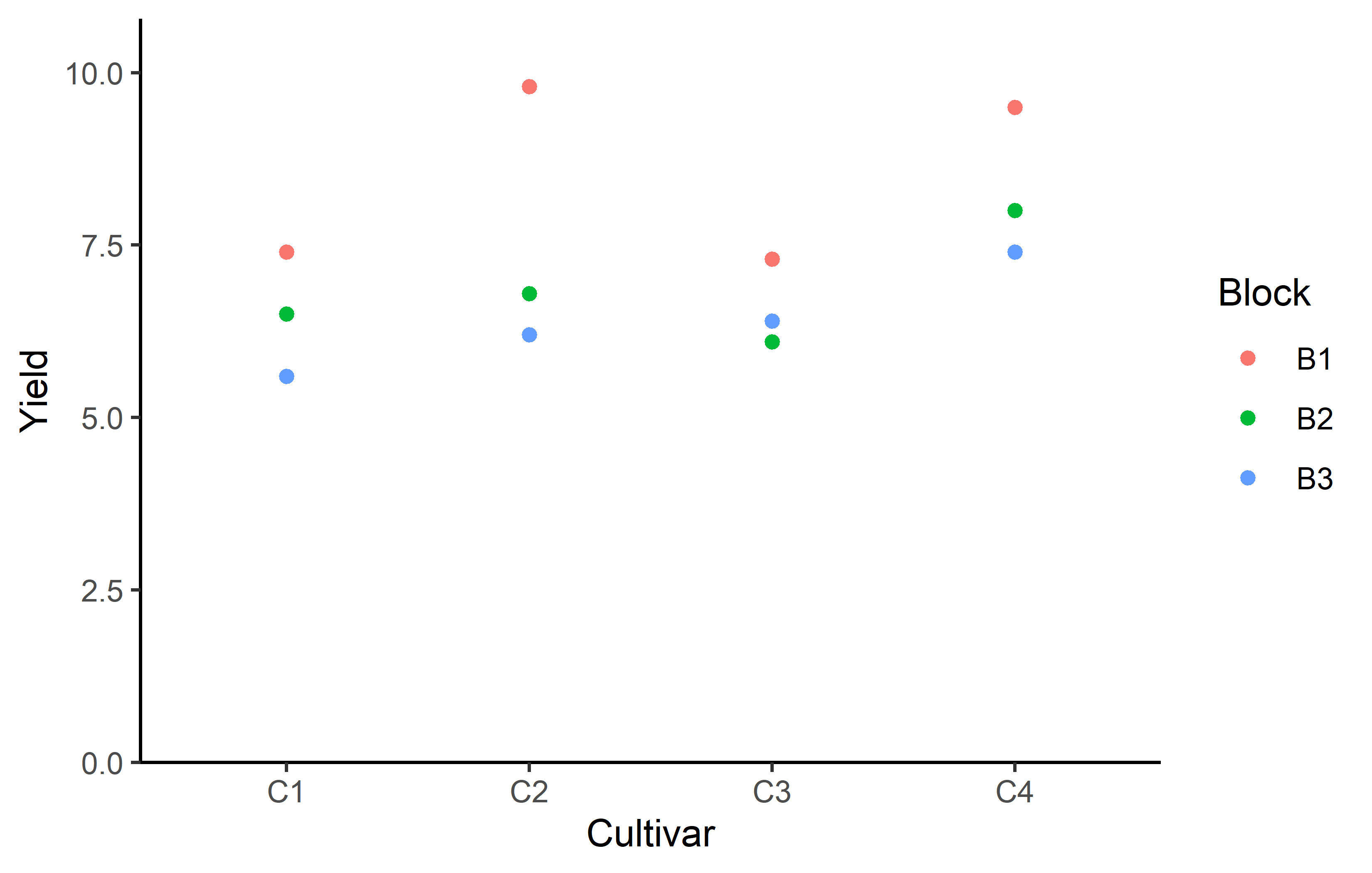
3 B3 4 0 6.4 0.748Additionally, we can decide to plot our data:
Code
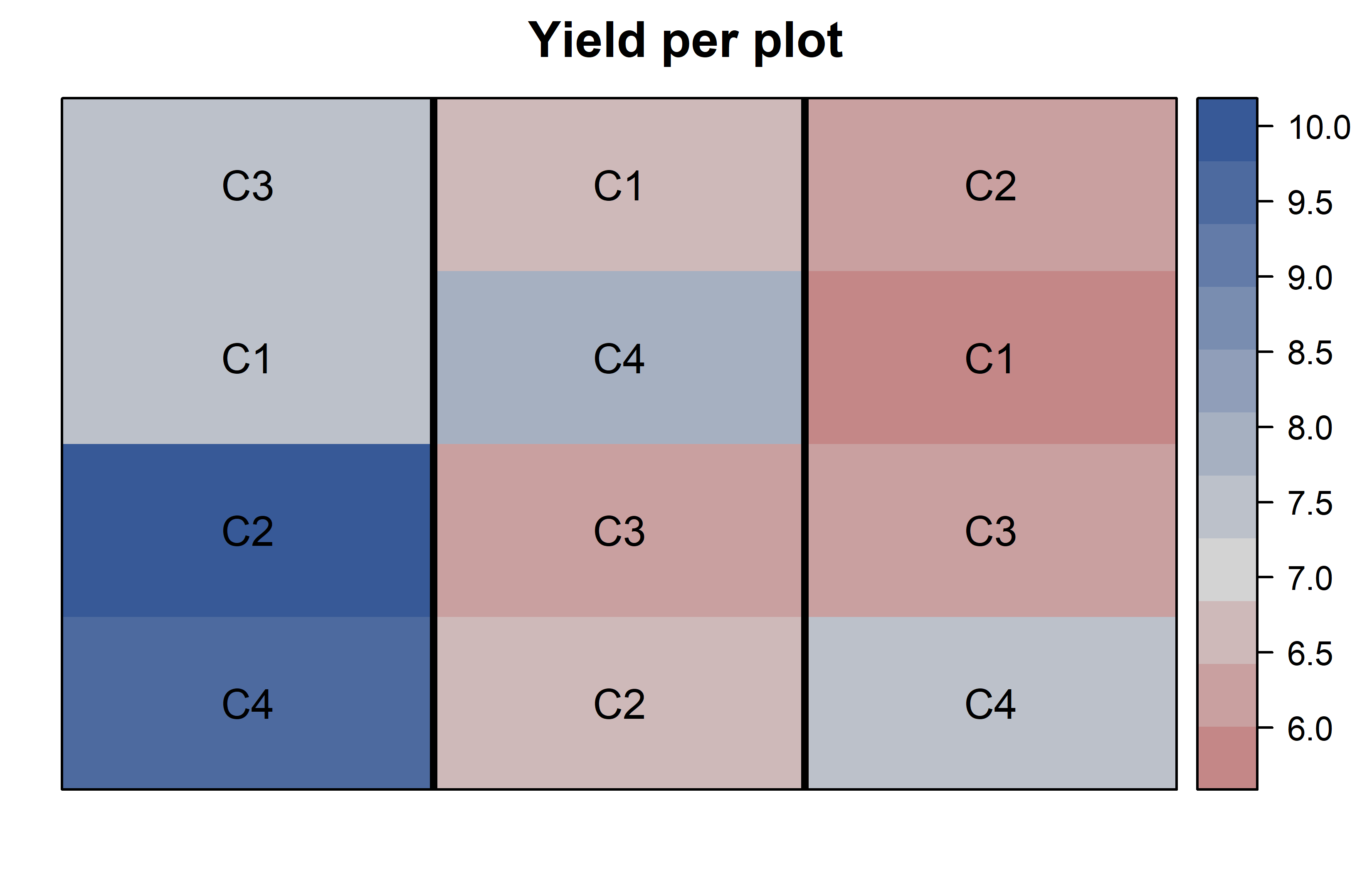
Finally, since this is an experiment that was laid with a certain experimental design (= a randomized complete block design; RCBD) - it makes sense to also get a field plan. This can be done via desplot() from {desplot}. We can even create a second field plan that gives us a feeling for the yields per plot.
Code
desplot(
data = dat,
flip = TRUE, # row 1 on top, not on bottom
form = cultivar ~ col + row, # fill color per cultivar
out1 = block, # line between blocks
text = cultivar, # cultivar names per plot
cex = 1, # cultviar names: font size
shorten = FALSE, # cultivar names: don't abbreviate
main = "Field layout: cultivars", # plot title
show.key = FALSE # hide legend
) Code
desplot(
data = dat,
flip = TRUE, # row 1 on top, not on bottom
form = yield ~ col + row, # fill color according to yield
out1 = block, # line between blocks
text = cultivar, # cultivar names per plot
cex = 1, # cultviar names: font size
shorten = FALSE, # cultivar names: don't abbreviate
main = "Yield per plot", # plot title
show.key = FALSE # hide legend
) Thus, C4 seems to be the most promising cultivar in terms of yield. Moreover, it can be seen that yields were generally higher in block B1 (left), compared to the other blocks.
Model
Finally, we can decide to fit a linear model with yield as the response variable and (fixed) cultivar and block effects.
mod <- lm(yield ~ cultivar + block, data = dat)It would be at this moment (i.e. after fitting the model and before running the ANOVA), that you should check whether the model assumptions are met. Find out more in the summary article “Model Diagnostics”
ANOVA
Based on our model, we can then conduct an ANOVA:
ANOVA <- anova(mod)
ANOVAAnalysis of Variance Table
Response: yield
Df Sum Sq Mean Sq F value Pr(>F)
cultivar 3 6.63 2.21 5.525 0.036730 *
block 2 9.78 4.89 12.225 0.007651 **
Residuals 6 2.40 0.40
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Accordingly, the ANOVA’s F-test found the cultivar effects to be statistically significant (p = 0.037*). Additionally, the block effects are also statistically significant (p = 0.008**), but this is only of secondary concern for us.
Mean comparison
Besides an ANOVA, one may also want to compare adjusted yield means between cultivars via post hoc tests (t-test, Tukey test etc.).
mean_comp <- mod %>%
emmeans(specs = ~ cultivar) %>% # adj. mean per cultivar
cld(adjust = "none", Letters = letters) # compact letter display (CLD)
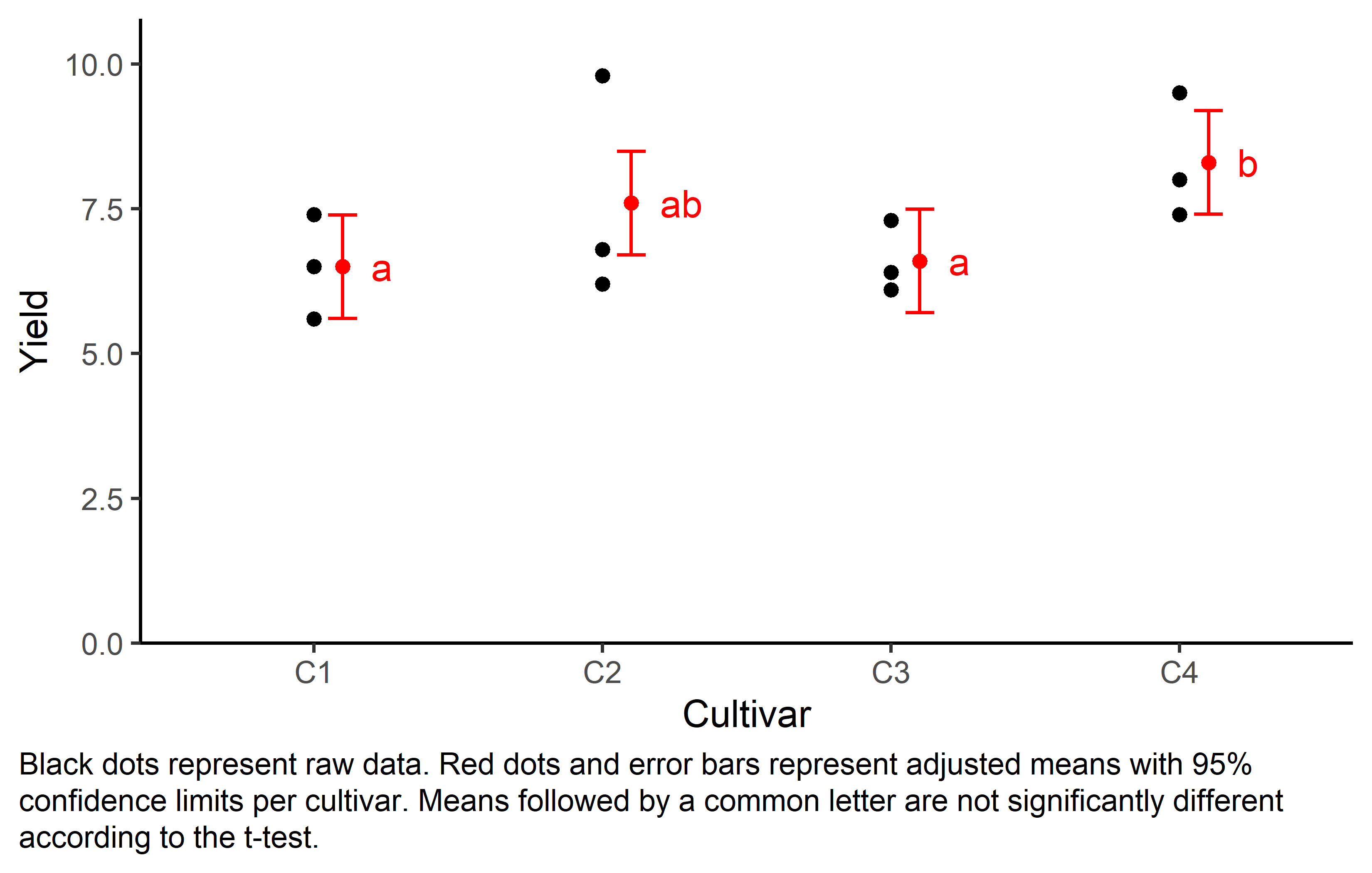
mean_comp cultivar emmean SE df lower.CL upper.CL .group
C1 6.5 0.365 6 5.61 7.39 a
C3 6.6 0.365 6 5.71 7.49 a
C2 7.6 0.365 6 6.71 8.49 ab
C4 8.3 0.365 6 7.41 9.19 b
Results are averaged over the levels of: block
Confidence level used: 0.95
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. Note that if you would like to see the underlying individual contrasts/differences between adjusted means, simply add details = TRUE to the cld() statement. Furthermore, check out the Summary Article “Compact Letter Display”.
Finally, we can create a plot that displays both the raw data and the results, i.e. the comparisons of the adjusted means that are based on the linear model.
Code
my_caption <- "Black dots represent raw data. Red dots and error bars represent adjusted means with 95% confidence limits per cultivar. Means followed by a common letter are not significantly different according to the t-test."
ggplot() +
aes(x = cultivar) +
# black dots representing the raw data
geom_point(
data = dat,
aes(y = yield)
) +
# red dots representing the adjusted means
geom_point(
data = mean_comp,
aes(y = emmean),
color = "red",
position = position_nudge(x = 0.1)
) +
# red error bars representing the confidence limits of the adjusted means
geom_errorbar(
data = mean_comp,
aes(ymin = lower.CL, ymax = upper.CL),
color = "red",
width = 0.1,
position = position_nudge(x = 0.1)
) +
# red letters
geom_text(
data = mean_comp,
aes(y = emmean, label = str_trim(.group)),
color = "red",
position = position_nudge(x = 0.2),
hjust = 0
) +
scale_x_discrete(
name = "Cultivar"
) +
scale_y_continuous(
name = "Yield",
limits = c(0, NA),
expand = expansion(mult = c(0, 0.1))
) +
scale_color_discrete(
name = "Block"
) +
theme_classic() +
labs(caption = my_caption) +
theme(plot.caption = element_textbox_simple(margin = margin(t = 5)),
plot.caption.position = "plot")References
Citation
@online{schmidt2023,
author = {Paul Schmidt},
title = {One-Way Randomized Complete Block Design},
date = {2023-11-16},
url = {https://schmidtpaul.github.io/dsfair_quarto//ch/exan/simple/rcbd_clewerscarisbrick2001.html},
langid = {en},
abstract = {One-way ANOVA \& pairwise comparison post hoc tests in a
randomized complete block design.}
}