# packages
pacman::p_load(agridat, tidyverse, # data import and handling
               conflicted, # handling function conflicts
               emmeans, multcomp, multcompView, # adjusted mean comparisons
               ggplot2, desplot) # plots

# conflicts: identical function names from different packages
conflict_prefer("filter", "dplyr")
conflict_prefer("select", "dplyr")

Data

This example is taken from the agridat: Agricultural Datasets package. It considers data published in Bridges (1989) from a cucumber yield trial set up as a latin square design. Notice that the original dataset considers two trials (at two locations), but we will focus on only a single trial here.

Import

# data (from agridat package)
dat <- agridat::bridges.cucumber %>% 
  filter(loc == "Clemson") %>% # subset data from only one location
  select(-loc) # remove loc column which is now unnecessary

dat

##         gen row col yield
## 1    Dasher   1   3  44.2
## 2    Dasher   2   4  54.1
## 3    Dasher   3   2  47.2
## 4    Dasher   4   1  36.7
## 5  Guardian   1   4  33.0
## 6  Guardian   2   2  13.6
## 7  Guardian   3   1  44.1
## 8  Guardian   4   3  35.8
## 9  Poinsett   1   1  11.5
## 10 Poinsett   2   3  22.4
## 11 Poinsett   3   4  30.3
## 12 Poinsett   4   2  21.5
## 13   Sprint   1   2  15.1
## 14   Sprint   2   1  20.3
## 15   Sprint   3   3  41.3
## 16   Sprint   4   4  27.1

Formatting

While gen is already correctly encoded as factor, the columns row and col should be encoded as factors, too, since R by default encoded them as integer. However, we also want to keep row and col as integer for the desplot() function. Therefore we create copies of these columns encoded as factors and named rowF and colF

dat <- dat %>% 
  as_tibble() %>% # tibble data format for convenience
  mutate(rowF = row %>% as.factor,
         colF = col %>% as.factor)

Exploring

In order to obtain a field layout of the trial, we can use the desplot() function. Notice that for this we need two data columns that identify the row and col of each plot in the trial.

desplot(data = dat, flip = TRUE,
        form = gen ~ row + col, 
        out1 = row, out1.gpar=list(col="black", lwd=3),
        out2 = col, out2.gpar=list(col="black", lwd=3),
        text = gen, cex = 1, shorten = "no",
        main = "Field layout", 
        show.key = FALSE)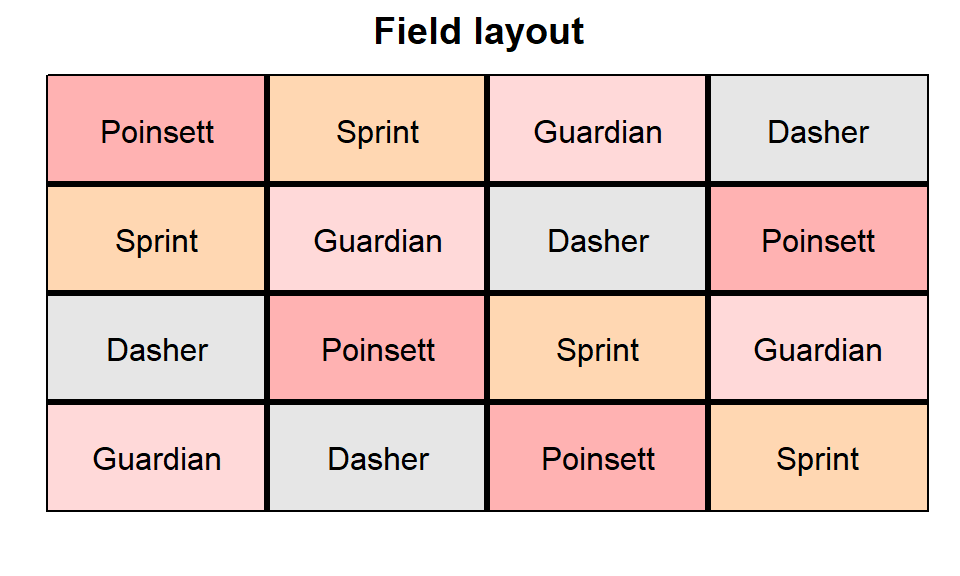

We could also have a look at the arithmetic means and standard deviations for yield per genotype, row or col.

dat %>% 
  group_by(gen) %>% # genotype
  summarize(mean    = mean(yield),
            std.dev = sd(yield)) %>% 
  arrange(desc(mean))

## # A tibble: 4 × 3
##   gen       mean std.dev
##   <fct>    <dbl>   <dbl>
## 1 Dasher    45.6    7.21
## 2 Guardian  31.6   12.9 
## 3 Sprint    26.0   11.4 
## 4 Poinsett  21.4    7.71

dat %>% 
  group_by(row) %>% # row
  summarize(mean    = mean(yield),
            std.dev = sd(yield))

## # A tibble: 4 × 3
##     row  mean std.dev
##   <int> <dbl>   <dbl>
## 1     1  26.0   15.4 
## 2     2  27.6   18.1 
## 3     3  40.7    7.36
## 4     4  30.3    7.28

dat %>% 
  group_by(col) %>% # column
  summarize(mean    = mean(yield),
            std.dev = sd(yield))

## # A tibble: 4 × 3
##     col  mean std.dev
##   <int> <dbl>   <dbl>
## 1     1  28.2   14.9 
## 2     2  24.4   15.6 
## 3     3  35.9    9.67
## 4     4  36.1   12.2

We can also create a plot to get a better feeling for the data.

ggplot(data = dat,
       aes(y = yield, x = gen, color = rowF, shape=colF)) +
  geom_point(size=2) +  # scatter plot with larger points
  ylim(0, NA) +   # force y-axis to start at 0
  theme_classic() # clearer plot format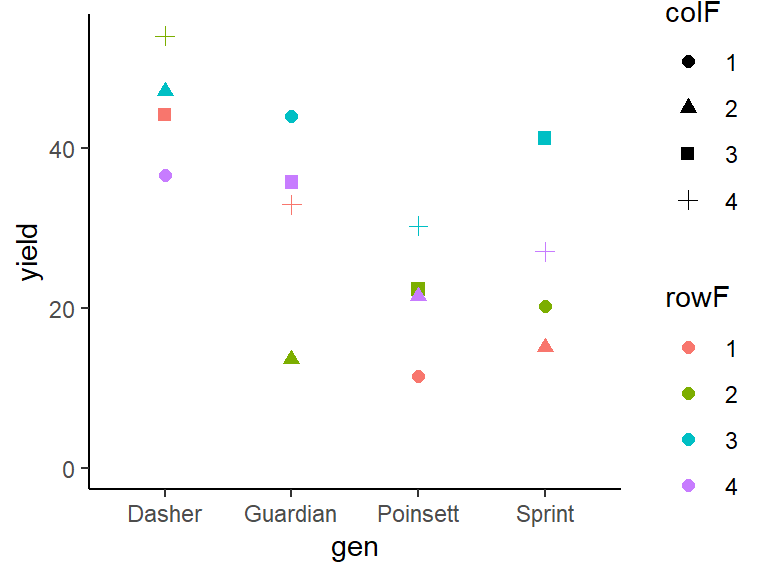

Modelling

Finally, we can decide to fit a linear model with yield as the response variable and (fixed) gen effects, as well as rowF and colF effects. Important: Don’t forget to use the variables for rows and columns that are encoded as factors and thus not the ones used in the desplot() function above.

mod <- lm(yield ~ gen + rowF + colF, data = dat)

ANOVA

Thus, we can conduct an ANOVA for this model. As can be seen, the F-test of the ANOVA finds the gen effects to be statistically significant (p = 0.011 < 0.05).

mod %>% anova()

## Analysis of Variance Table
## 
## Response: yield
##           Df  Sum Sq Mean Sq F value  Pr(>F)  
## gen        3 1316.80  438.93  9.3683 0.01110 *
## rowF       3  528.35  176.12  3.7589 0.07872 .
## colF       3  411.16  137.05  2.9252 0.12197  
## Residuals  6  281.12   46.85                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Mean comparisons

Following a significant F-test, one will want to compare genotype means.

mean_comparisons <- mod %>% 
  emmeans(specs = "gen") %>% # get adjusted means for cultivars
  cld(adjust="tukey", Letters=letters) # add compact letter display

mean_comparisons

##  gen      emmean   SE df lower.CL upper.CL .group
##  Poinsett   21.4 3.42  6     9.43     33.4  a    
##  Sprint     25.9 3.42  6    13.95     37.9  a    
##  Guardian   31.6 3.42  6    19.63     43.6  ab   
##  Dasher     45.5 3.42  6    33.55     57.5   b   
## 
## Results are averaged over the levels of: rowF, colF 
## Confidence level used: 0.95 
## Conf-level adjustment: sidak method for 4 estimates 
## P value adjustment: tukey method for comparing a family of 4 estimates 
## significance level used: alpha = 0.05 
## NOTE: If two or more means share the same grouping symbol,
##       then we cannot show them to be different.
##       But we also did not show them to be the same.

Note that if you would like to see the underyling individual contrasts/differences between adjusted means, simply add details = TRUE to the cld() statement. Also, find more information on mean comparisons and the Compact Letter Display in the separate Compact Letter Display Chapter

Present results

Mean comparisons

For this example we can create a plot that displays both the raw data and the results, i.e. the comparisons of the adjusted means that are based on the linear model. If you would rather have e.g. a bar plot to show these results, check out the separate Compact Letter Display Chapter

ggplot() +
  # black dots representing the raw data
  geom_point(
    data = dat,
    aes(y = yield, x = gen)
  ) +
  # red dots representing the adjusted means
  geom_point(
    data = mean_comparisons,
    aes(y = emmean, x = gen),
    color = "red",
    position = position_nudge(x = 0.1)
  ) +
  # red error bars representing the confidence limits of the adjusted means
  geom_errorbar(
    data = mean_comparisons,
    aes(ymin = lower.CL, ymax = upper.CL, x = gen),
    color = "red",
    width = 0.1,
    position = position_nudge(x = 0.1)
  ) +
  # red letters 
  geom_text(
    data = mean_comparisons,
    aes(y = emmean, x = gen, label = .group),
    color = "red",
    position = position_nudge(x = 0.2)
  ) + 
  ylim(0, NA) + # force y-axis to start at 0
  ylab("Yield") + # label y-axis
  xlab("Cucumber genotype") + # label x-axis
  labs(caption = "Black dots represent raw data
       Red dots and error bars represent adjusted mean with 95% confidence limits per genotype
       Means followed by a common letter are not significantly different according to the Tukey-test") +
  theme_classic() # clearer plot format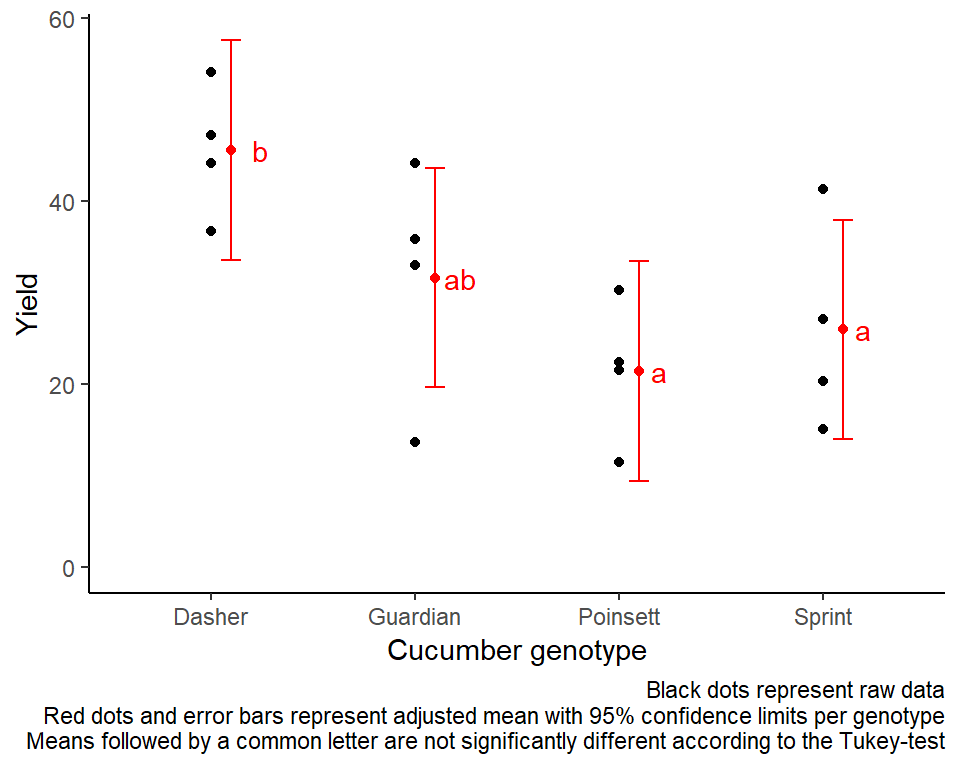

R-Code and exercise solutions

Please click here to find a folder with .R files. Each file contains

the entire R-code of each example combined, including
solutions to the respective exercise(s).

Please feel free to contact me about any of this!

schmidtpaul1989@outlook.com

There is a newer, revised version of this website: https://schmidtpaul.github.io/dsfair_quarto/

Latin square design

Data

Import

Formatting

Exploring

Modelling

ANOVA

Mean comparisons

Present results

Mean comparisons