# packages
pacman::p_load(tidyverse, # data import and handling
               conflicted, # handling function conflicts
               emmeans, multcomp, multcompView, # adjusted mean comparisons
               ggplot2, desplot) # plots

Data

This data is a slightly modified version of that in the split-plot chapter published in Gomez & Gomez (1984) from a yield (kg/ha) trial with 4 genotypes (G) and 6 nitrogen levels (N), leading to 24 treatment level combinations. The data set here has 3 complete replicates (rep) and is laid out as a randomized complete block design (RCBD).

Import

# data (import via URL)
dataURL <- "https://raw.githubusercontent.com/SchmidtPaul/DSFAIR/master/data/riceRCBD.csv"
dat <- read_csv(dataURL)

dat

## # A tibble: 72 × 6
##      row   col rep   N     G     yield
##    <dbl> <dbl> <chr> <chr> <chr> <dbl>
##  1     2     6 rep1  N1    A      4520
##  2     3     4 rep1  N2    A      5598
##  3     2     3 rep1  N4    A      6192
##  4     1     1 rep1  N6    A      8542
##  5     2     1 rep1  N3    A      5806
##  6     3     1 rep1  N5    A      7470
##  7     4     5 rep1  N1    B      4034
##  8     4     1 rep1  N2    B      6682
##  9     3     2 rep1  N4    B      6869
## 10     1     2 rep1  N6    B      6318
## # … with 62 more rows

Formatting

Before anything, the columns rep, N and G should be encoded as factors, since R by default encoded them as character.

dat <- dat %>% 
  mutate_at(vars(rep, N, G), as.factor)

Exploring

In order to obtain a field layout of the trial, we can use the desplot() function. Notice that for this we need two data columns that identify the row and col of each plot in the trial.

desplot(data = dat,
        form = rep ~ col + row | rep, # fill color per rep, headers per rep
        text = G, cex = 1, shorten = "no", # show genotype names per plot
        col  = N, # color of genotype names for each N-level
        out1 = col, out1.gpar = list(col = "darkgrey"), # lines between columns
        out2 = row, out2.gpar = list(col = "darkgrey"), # lines between rows
        main = "Field layout", show.key = TRUE, key.cex = 0.7) # formatting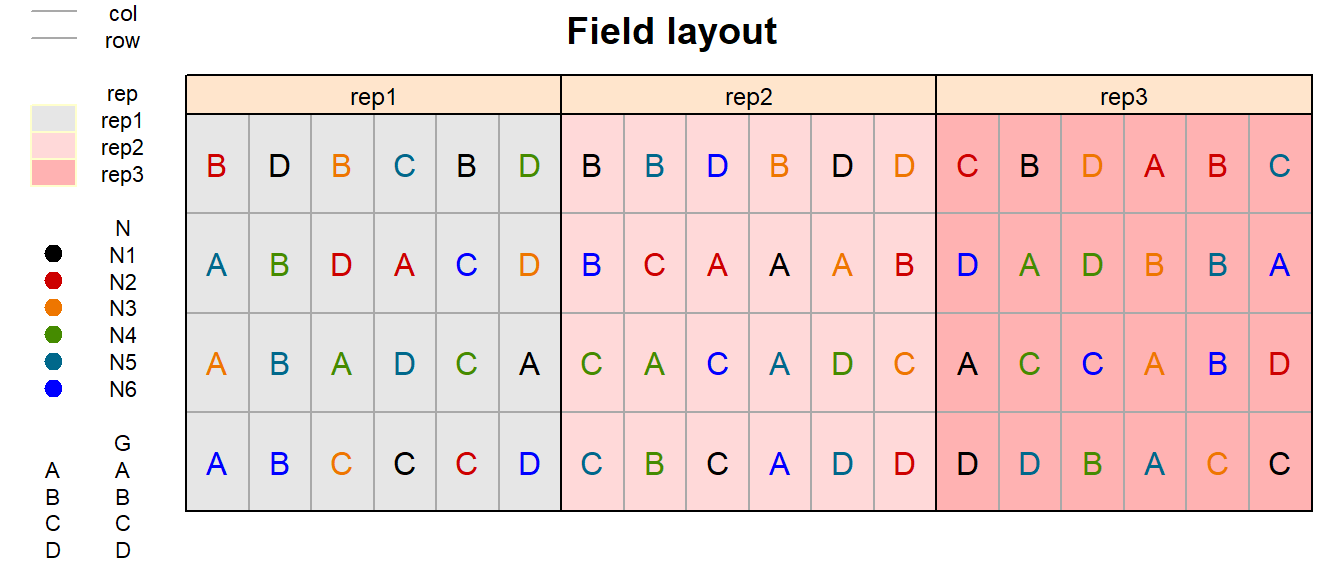

Just as in a RCBD for a single treatment factor, a RCBD for two treatment factors has replicates arranged as complete blocks. Thus, all 24 treatment level combinations are grouped together in three complete blocks, respectively.

We could now have a look at the arithmetic means and standard deviations for yield per genotype (G) and nitrogen level (N) separately, but also for their combinations:

dat %>% 
  group_by(G) %>% 
  summarize(mean    = mean(yield),
            std.dev = sd(yield)) %>% 
  arrange(desc(mean))

## # A tibble: 4 × 3
##   G      mean std.dev
##   <fct> <dbl>   <dbl>
## 1 A     6554.   1475.
## 2 B     6156.   1078.
## 3 C     5563.   1269.
## 4 D     3642.   1434.

dat %>% 
  group_by(N) %>% 
  summarize(mean    = mean(yield),
            std.dev = sd(yield)) %>% 
  arrange(desc(mean))

## # A tibble: 6 × 3
##   N      mean std.dev
##   <fct> <dbl>   <dbl>
## 1 N3    5866.    832.
## 2 N4    5864.   1434.
## 3 N5    5812    2349.
## 4 N6    5797.   2660.
## 5 N2    5478.    657.
## 6 N1    4054.    672.

dat %>% 
  group_by(N, G) %>% 
  summarize(mean    = mean(yield),
            std.dev = sd(yield)) %>% 
  arrange(desc(mean)) %>% 
  print(n=Inf) # show more than default 10 rows

## # A tibble: 24 × 4
## # Groups:   N [6]
##    N     G      mean std.dev
##    <fct> <fct> <dbl>   <dbl>
##  1 N6    A     8701.   270. 
##  2 N5    A     7563.    86.9
##  3 N5    B     6951.   808. 
##  4 N4    B     6895    166. 
##  5 N4    A     6733.   490. 
##  6 N5    C     6687.   496. 
##  7 N6    B     6540.   936. 
##  8 N3    A     6400    523. 
##  9 N3    B     6259    499. 
## 10 N6    C     6065.  1097. 
## 11 N4    C     6014    515. 
## 12 N3    C     5994    101. 
## 13 N2    B     5982    684. 
## 14 N2    A     5672    458. 
## 15 N2    C     5443.   589. 
## 16 N2    D     4816    506. 
## 17 N3    D     4812    963. 
## 18 N1    D     4481.   463. 
## 19 N1    B     4306    646. 
## 20 N1    A     4253.   248. 
## 21 N4    D     3816   1311. 
## 22 N1    C     3177.   453. 
## 23 N5    D     2047.   703. 
## 24 N6    D     1881.   407.

We can also create a plot to get a better feeling for the data.

ggplot(
  data = dat,
  aes(
    y = yield,
    x = N,
    color = N
  )
) +
  facet_wrap(~G, labeller = label_both) + # facette per G level
  geom_point() + # dots representing the raw data
  scale_y_continuous(
    limits = c(0, NA), # make y-axis start at 0
    expand = expansion(mult = c(0, 0.1)) # no space below 0
  ) +
  scale_x_discrete(name = NULL) + # x-axis
  theme_bw() + # clearer plot format
  theme(legend.position = "bottom") # legend on top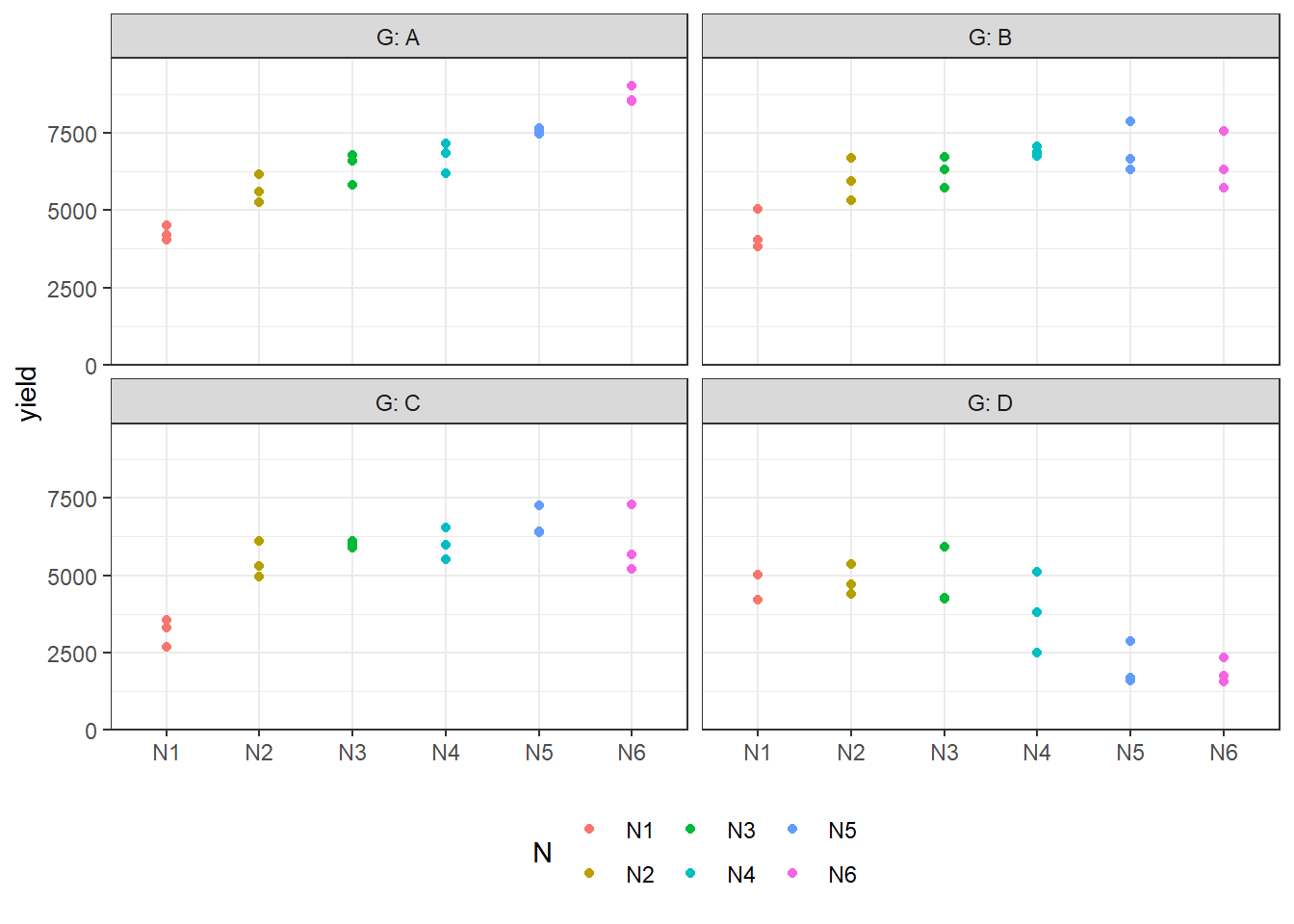

Modelling

Finally, we can decide to fit a linear model with yield as the response variable. In this example it makes sense to mentally group the effects in our model as either design effects or treatment effects. The treatments here are the genotypes G and the nitrogen levels N which we will include in the model as main effects, but also via their interaction effect N:G. Regarding the design, the model needs to contain a block (rep) effect.

mod <- lm(
  yield ~ N + G + N:G + rep,
  data = dat
)

Hint: N*G is short for N + G + N:G.

ANOVA

As a next step, we can conduct an ANOVA for this model.

anova(mod)

## Analysis of Variance Table
## 
## Response: yield
##           Df   Sum Sq  Mean Sq F value    Pr(>F)    
## N          5 30480453  6096091 15.4677 6.509e-09 ***
## G          3 89885035 29961678 76.0221 < 2.2e-16 ***
## rep        2  1084820   542410  1.3763    0.2627    
## N:G       15 69378044  4625203 11.7356 4.472e-11 ***
## Residuals 46 18129432   394118                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Whenever we have multiple treatment effects in a model, we should focus on the term with the highest complexity when it comes to the ANOVA. In this case, this is the N:G interaction effect and its F-test is significant (p<0.001).

As a result, we should only compares means for the 24 genotype-nitrogen-combinations (“cell means”) and not for the 6 nitrogens across the genotypes or 4 genotypes across the nitrogens (“marginal means”). This is because marginal means are misleading in the presence of interaction.

Do not confuse “marginal means” with “estimated marginal means (emmeans)”. Both, cell means and marginal means can be estimated via emmeans::emmeans().

Mean comparisons

Accordingly, we will proceed comparing the 24 means for N:G. Whenever means of a two-way treatment interaction such as this are to be compared, I choose between two options, which are both valid but one may be more apt to answer the question at hand:

~ N:G Comparing all combinations to all other combinations
~ N|G Comparing all genotype means per nitrogen (or the other way around)

Option 1: `~ N:G`

Here, we really calculate and test all of the 276 possible differences between the 24 nitrogen-genotype combination means.

all_mean_comparisons <- mod %>%
  emmeans(specs = ~ N:G) %>% # compare all combs to all other combs
  cld(adjust = "none", Letters = letters) # add compact letter display

all_mean_comparisons

##  N  G emmean  SE df lower.CL upper.CL .group     
##  N6 D   1881 362 46     1151     2610  a         
##  N5 D   2047 362 46     1317     2776  a         
##  N1 C   3177 362 46     2448     3907   b        
##  N4 D   3816 362 46     3086     4546   bc       
##  N1 A   4253 362 46     3523     4982    c       
##  N1 B   4306 362 46     3576     5036    c       
##  N1 D   4481 362 46     3752     5211    cd      
##  N3 D   4812 362 46     4082     5542    cde     
##  N2 D   4816 362 46     4086     5546    cde     
##  N2 C   5443 362 46     4713     6172     def    
##  N2 A   5672 362 46     4942     6402      efg   
##  N2 B   5982 362 46     5252     6712       fgh  
##  N3 C   5994 362 46     5264     6724       fgh  
##  N4 C   6014 362 46     5284     6744       fgh  
##  N6 C   6065 362 46     5336     6795       fgh  
##  N3 B   6259 362 46     5529     6989       fgh  
##  N3 A   6400 362 46     5670     7130       fgh  
##  N6 B   6540 362 46     5811     7270        ghi 
##  N5 C   6687 362 46     5958     7417        ghi 
##  N4 A   6733 362 46     6003     7462         hi 
##  N4 B   6895 362 46     6165     7625         hi 
##  N5 B   6951 362 46     6221     7680         hi 
##  N5 A   7563 362 46     6834     8293          i 
##  N6 A   8701 362 46     7971     9430           j
## 
## Results are averaged over the levels of: rep 
## Confidence level used: 0.95 
## significance level used: alpha = 0.05 
## NOTE: If two or more means share the same grouping symbol,
##       then we cannot show them to be different.
##       But we also did not show them to be the same.

all_mean_comparisons <- all_mean_comparisons %>% 
  as_tibble() %>%
  mutate(N_G = paste0(N, "-", G)) %>% # create helper column with combs
  mutate(N_G = fct_reorder(N_G, emmean)) # sort combs according to emmean

# do the same for the raw data
dat <- dat %>% 
  mutate(N_G = paste0(N, "-", G)) %>% 
  mutate(N_G = fct_relevel(N_G, levels(all_mean_comparisons$N_G)))


ggplot() +
  # dots representing the raw data
  geom_point(
    data = dat,
    aes(y = yield, x = N_G, color = N),
    position = position_nudge(x = -0.2)
  ) +
  # black boxplot
  geom_boxplot(
    data = dat,
    aes(y = yield, x = N_G),
    width = 0.05,
    outlier.shape = NA,
    position = position_nudge(x = -0.1)
  ) +
  # red mean value
  geom_point(
    data = all_mean_comparisons,
    aes(y = emmean, x = N_G),
    size = 2,
    color = "red"
  ) +
  # red mean errorbar
  geom_errorbar(
    data = all_mean_comparisons,
    aes(ymin = lower.CL, ymax = upper.CL, x = N_G),
    width = 0.05,
    color = "red"
  ) +
  # red letters
  geom_text(
    data = all_mean_comparisons,
    aes(
      y = 10000,
      x = N_G,
      label = .group
    ),
    angle = 90,
    hjust = 0,
    color = "red"
  ) +
  # y-axis
  scale_y_continuous(
    name = "Yield",
    limits = c(0, 12500),
    expand = expansion(mult = c(0, 0.1))
  ) +
  # x-axis
  scale_x_discrete(name = "Nitrogen-Genotype combination") +
  # general layout
  theme_bw() +
  theme(
    axis.text.x = element_text(
      angle = 45,
      hjust = 1,
      vjust = 1
    ),
    legend.position = "bottom"
  ) +
  labs(
    caption = str_wrap("Black dots represent raw data. Red dots and error bars represent estimated marginal means ± 95% confidence interval per group. Means not sharing any letter are significantly different by the t-test at the 5% level of significance.", width = 120)
  )

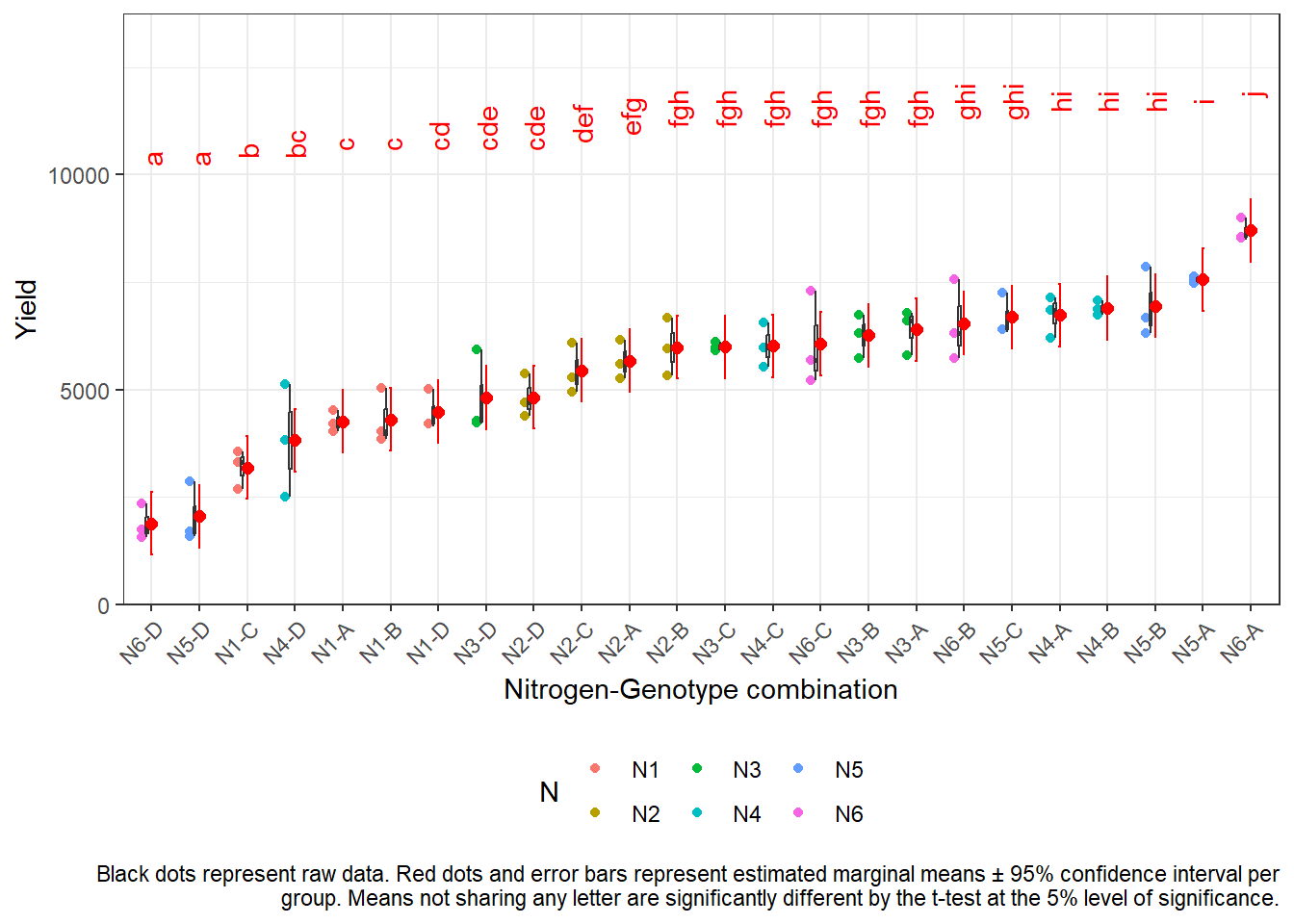
As can be seen, this option can lead to overwhelming results when there are too many treatment level combinations.

Option 2: `~ N|G`

Here, we only calculate and test 60 differences between the 24 nitrogen-genotype combination means, since - separately for each of the 4 genotypes - we only compare all 6 nitrogen means to each other, leading to 4x15=60 comparisons. (Note that you may analogously switch N|G to G|N and instead present results for these 6x6=36 comparisons, if they seem more apt for your research question.)

withinG_mean_comparisons <- mod %>%
  emmeans(specs = ~ N|G) %>% 
  cld(adjust="none", Letters=letters) # add compact letter display

withinG_mean_comparisons

## G = A:
##  N  emmean  SE df lower.CL upper.CL .group
##  N1   4253 362 46     3523     4982  a    
##  N2   5672 362 46     4942     6402   b   
##  N3   6400 362 46     5670     7130   bc  
##  N4   6733 362 46     6003     7462    cd 
##  N5   7563 362 46     6834     8293     d 
##  N6   8701 362 46     7971     9430      e
## 
## G = B:
##  N  emmean  SE df lower.CL upper.CL .group
##  N1   4306 362 46     3576     5036  a    
##  N2   5982 362 46     5252     6712   b   
##  N3   6259 362 46     5529     6989   b   
##  N6   6540 362 46     5811     7270   b   
##  N4   6895 362 46     6165     7625   b   
##  N5   6951 362 46     6221     7680   b   
## 
## G = C:
##  N  emmean  SE df lower.CL upper.CL .group
##  N1   3177 362 46     2448     3907  a    
##  N2   5443 362 46     4713     6172   b   
##  N3   5994 362 46     5264     6724   bc  
##  N4   6014 362 46     5284     6744   bc  
##  N6   6065 362 46     5336     6795   bc  
##  N5   6687 362 46     5958     7417    c  
## 
## G = D:
##  N  emmean  SE df lower.CL upper.CL .group
##  N6   1881 362 46     1151     2610  a    
##  N5   2047 362 46     1317     2776  a    
##  N4   3816 362 46     3086     4546   b   
##  N1   4481 362 46     3752     5211   b   
##  N3   4812 362 46     4082     5542   b   
##  N2   4816 362 46     4086     5546   b   
## 
## Results are averaged over the levels of: rep 
## Confidence level used: 0.95 
## significance level used: alpha = 0.05 
## NOTE: If two or more means share the same grouping symbol,
##       then we cannot show them to be different.
##       But we also did not show them to be the same.

withinG_mean_comparisons <- as_tibble(withinG_mean_comparisons)

ggplot() +
  facet_wrap(~G, labeller = label_both) + # facette per G level
  # dots representing the raw data
  geom_point(
    data = dat,
    aes(y = yield, x = N, color = N)
  ) +
  # red dots representing the adjusted means
  geom_point(
    data = withinG_mean_comparisons,
    aes(y = emmean, x = N),
    color = "red",
    position = position_nudge(x = 0.1)
  ) +
  # red error bars representing the confidence limits of the adjusted means
  geom_errorbar(
    data = withinG_mean_comparisons,
    aes(ymin = lower.CL, ymax = upper.CL, x = N),
    color = "red",
    width = 0.1,
    position = position_nudge(x = 0.1)
  ) +
  # red letters
  geom_text(
    data = withinG_mean_comparisons,
    aes(y = emmean, x = N, label = str_trim(.group)),
    color = "red",
    hjust = 0,
    position = position_nudge(x = 0.2)
  ) +
  # y-axis
  scale_y_continuous(
    name = "Yield",
    limits = c(0, NA),
    expand = expansion(mult = c(0, 0.1))
  ) +
  # x-axis
  scale_x_discrete(name = NULL) +
  # general layout
  theme_bw() + # clearer plot format
  theme(legend.position = "bottom") + # legend on top
  labs(caption = str_wrap("The four facettes represent genotypes A, B, C and D. Black dots represent raw data. Red dots and error bars represent estimated marginal means ± 95% confidence interval per group. For each genotype separately, means not sharing any letter are significantly different by the t-test at the 5% level of significance.", width = 120))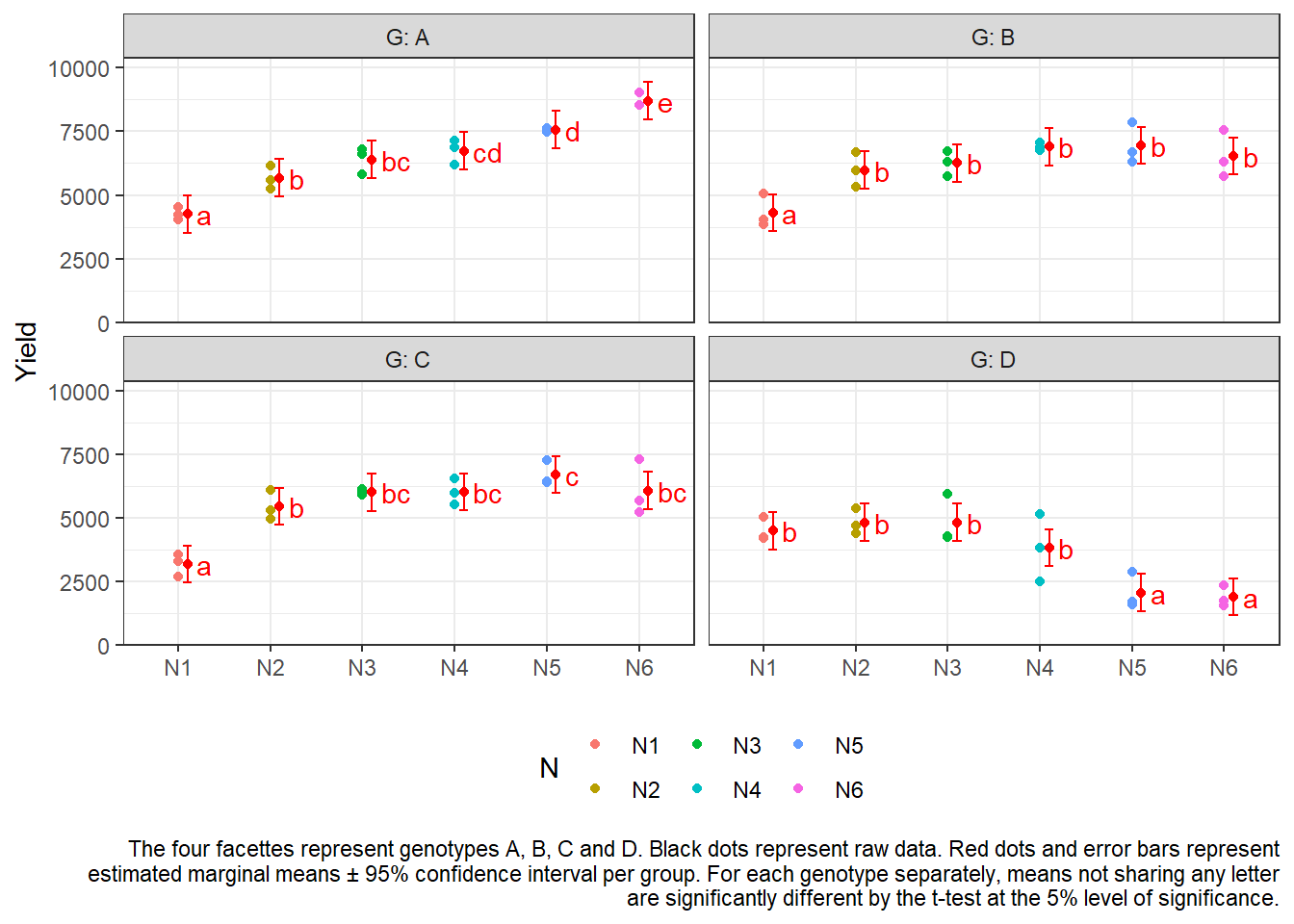

R-Code and exercise solutions

Please click here to find a folder with .R files. Each file contains

the entire R-code of each example combined, including
solutions to the respective exercise(s).

Please feel free to contact me about any of this!

schmidtpaul1989@outlook.com

There is a newer, revised version of this website: https://schmidtpaul.github.io/dsfair_quarto/

RCBD with 2 factors

Data

Import

Formatting

Exploring

Modelling

ANOVA

Mean comparisons

Option 1: `~ N:G`

Option 2: `~ N|G`

There is a newer, revised version of this website: https://schmidtpaul.github.io/dsfair_quarto/

RCBD with 2 factors

Data

Import

Formatting

Exploring

Modelling

ANOVA

Mean comparisons

Option 1: ~ N:G

Option 2: ~ N|G

Option 1: `~ N:G`

Option 2: `~ N|G`