Simple, lineare Regression
Ein zum Thema passendes Youtube Video gibt’s hier
Eine kurze Zusammenfassung
Der Begriff “Regression” kann für vieles stehen, meint aber oft den Spezialfall der einfachen, linearen Regression. Das Ziel einer solchen Regressionsanalyse ist es, wie bei der Korrelation, eine Beziehung zwischen zwei numerischen Variablen zu untersuchen. Allerdings besteht der Unterschied zur Korrelation darin, dass die Regression versucht die Beziehung der zwei Variablen zu modellieren. Es wird versucht eine beobachtete abhängige Variable (\(y\)) durch eine unabhängige Variable (\(x\)) zu erklären. Das Modell bei einer einfachen, linearen Regression lautet
\[ y = \alpha + \beta x \]
wobei \(\alpha\) bzw. \(a\) der Achsenabschnitt oder Intercept ist und \(\beta\) bzw. \(b\) die Steigung oder auch Slope. Kurz gesagt kann mit dem Herumspielen dieser zwei größen jede beliebige Gerade in einem Koordinatensystem gezeichnet werden.
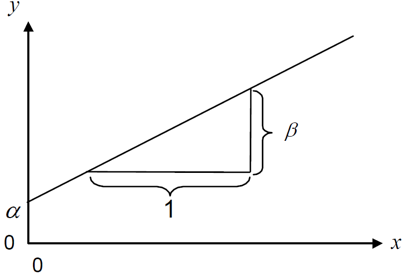
Zum Ausprobieren empfehle ich auf dieser Website ins Fenster oben links “y=a+bx” einzugeben, mit Enter zu bestätigen und dann an den Stellschrauben für \(a\) und \(b\) rumzuspielen.
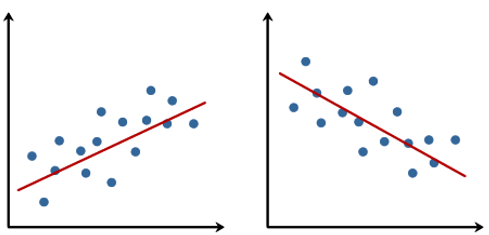
Bei einer Regressionsanalyse sollen schlichtweg die Werte für \(a\) und \(b\) gefunden werden, die am besten zu einer vorhandenen Punktewolke in einem Scatter Plot passen:
Bei Fragen kannst du mir gerne schreiben!
schmidtpaul@hotmail.de