Mit logistischer Regression oder Logit-Modell (von logistic unit) sind in der Regel Regressionsmodelle gemeint, die binäre Zielvariablen (z.B. Ja/Nein) modellieren. Streng genommen fallen aber auch die multinomiale (deutsch/englisch/spanisch; multinomial logistic regression) oder geordnete (schlecht/mittel/gut; ordered logit model) logistische Regressionen, also alle Regressionen mit diskreten Zielvariablen, in die Klasse der logistischen Regressionen, welche wiederum eine Untergruppe der generalisierten linearen Modelle sind.

Datensatz

Es wurde von insgesamt 18 Personen die Körpergröße in cm ermittelt. Unter den Personen waren 11 Frauen und 7 Männer:

heights

##     gender height
##  1:      F    165
##  2:      F    170
##  3:      F    159
##  4:      F    176
##  5:      F    172
##  6:      F    179
##  7:      F    174
##  8:      F    171
##  9:      F    173
## 10:      F    161
## 11:      F    160
## 12:      M    172
## 13:      M    190
## 14:      M    181
## 15:      M    175
## 16:      M    183
## 17:      M    189
## 18:      M    177

summary(heights)

##  gender     height     
##  F:11   Min.   :159.0  
##  M: 7   1st Qu.:170.2  
##         Median :173.5  
##         Mean   :173.7  
##         3rd Qu.:178.5  
##         Max.   :190.0

str(heights)

## Classes 'data.table' and 'data.frame':   18 obs. of  2 variables:
##  $ gender: Factor w/ 2 levels "F","M":..
##  $ height: int  165 170 159 176 172 17..
##  - attr(*, ".internal.selfref")=<exter..

Ziel der Analyse ist es, basierend auf der Körpergröße einer Person ihr Geschlecht zu schätzen. Anstelle eines Boxplots, sollen die Daten in diesem Fall wie folgt dargestellt werden:

library(ggplot2)
ggplot(data=heights, aes(x=height, y=gender, color=gender)) +
  geom_point() + theme_classic() +
  theme(legend.position = c(.9,.2),
        legend.box.background = element_rect(color = "black"))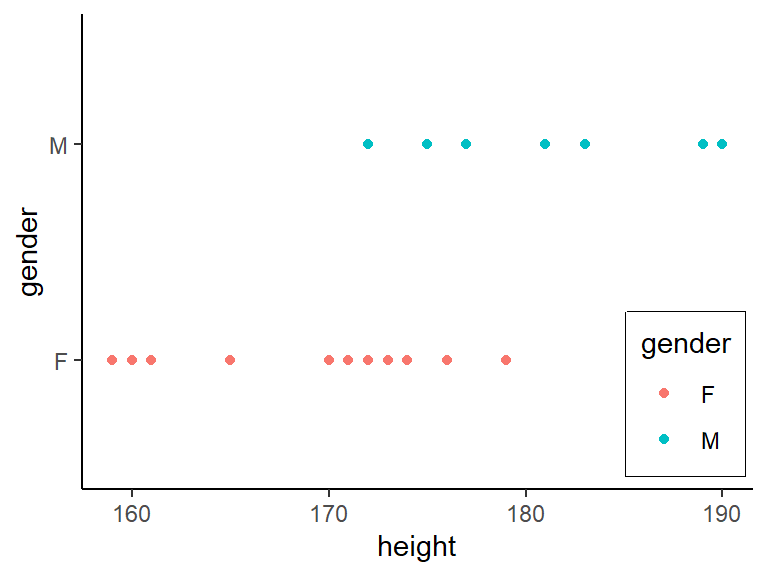

Analyse

Um für solch einen Datensatz eine Regression anzupassen, werden die Einträge der binären Zielvariable vorerst durch 0 und 1 ersetzt (sogenannte dummy-Codierung) und in der neuen Spalte dummy.gender gespeichert:

library(dplyr)
heights <- heights %>%
  mutate(dummy.gender = as.numeric(gender)-1)
heights[9:14,] # Zeige Zeilen 9-14

##    gender height dummy.gender
## 1:      F    173            0
## 2:      F    161            0
## 3:      F    160            0
## 4:      M    172            1
## 5:      M    190            1
## 6:      M    181            1

Weil unsere Zielvariable binär ist, also nur zwei verschiedene Werte annehmen kann (erst F/M, jetzt 0/1) wird klar, dass eine einfache Regression (\(y=\alpha+\beta x\)) keinen Sinn ergäbe, vor allem weil die Regression auch Werte <0% und >100% vorhersagen würde:

ggplot(data=heights, aes(x=height, y=dummy.gender)) + 
  theme_classic() +
  stat_smooth(method="lm", se=FALSE, color="red") +
  geom_point(aes(color=gender)) +
  ylab("Probability of person being male") +
  xlab("Person's height [cm]") +
  theme(legend.position=c(.9,.2),
        legend.box.background = element_rect(color = "black"))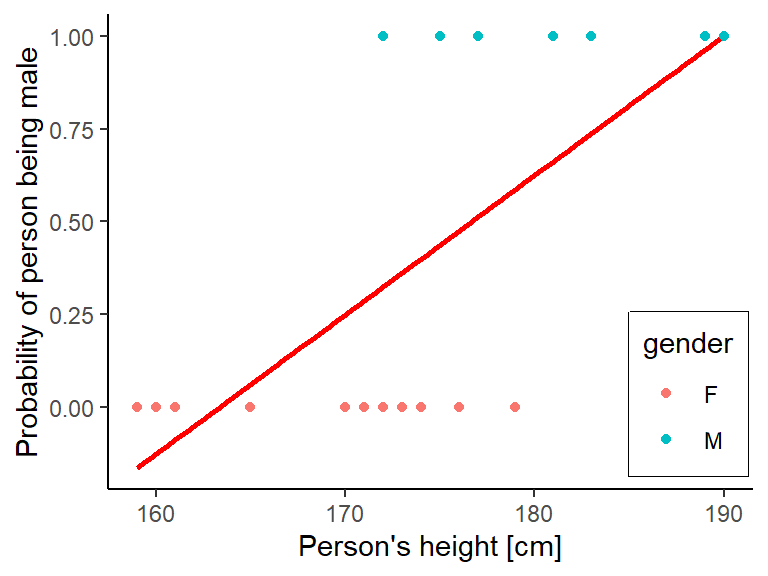

Stattdessen wird bei der logistischen Regression dafür gesorgt, dass quasi der Output der linearen Regression mittels der logistischen Regression zwischen 0 und 1 gequetscht wird. Die logistische Regression ist definiert als

\[ logistic(\eta) = \frac{1}{1+exp(-\eta)} \]

wobei \(\eta\) der lineare Prädiktor ist. In R kann eine logistische Regression mittels der glm Funktion und dem Argument family=binomial angepasst werden:

logit.mod <- glm(dummy.gender ~ height, 
                 family = binomial,
                 data = heights)

Auch die Darstellung im Plot ist leicht mit ggplot() möglich:

ggplot(data=heights, aes(x=height, y=dummy.gender)) + 
  theme_classic() +
  stat_smooth(method="glm", method.args=list(family="binomial"), 
              se=FALSE, color="darkgrey") +
  geom_point(aes(color=gender)) +
  ylab("Probability of person being male") +
  xlab("Person's height [cm]") +
  theme(legend.position=c(.9,.2),
        legend.box.background = element_rect(color = "black"))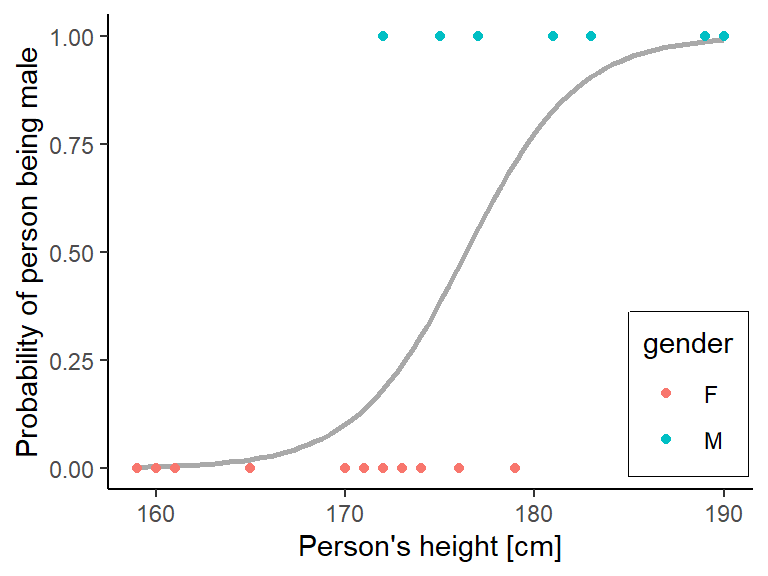

Das Modell kann nun also genutzt werden um anhand der Körpergröße einer Person zu schätzen ob diese Person ein Mann oder eine Frau ist. Als Beispiel können wir uns vom Modell vorhersagen lassen mit was für einer Wahrscheinlichkeit eine Person, die 180cm groß ist, ein Mann ist:

predict(logit.mod, data.frame(height=180), type="response")

##         1 
## 0.7744626

Die Antwortet lautet also: mit 77,4%iger Wahrscheinlichkeit.

Bei Fragen kannst du mir gerne schreiben!

schmidtpaul@hotmail.de

Logistische Regression

Datensatz

Analyse