Wechselwirkungen von Behandlungsfaktoren
In einem Experiment, in dem mehrere Behandlungsfaktoren geprüft werden, kann es sein, dass es Wechselwirkungen zwischen den Behandlungen gibt. Folgendes Beispiel soll demonstrieren was damit gemeint ist.
Zwei Behandlungsfaktoren
In einem Experiment (egal welches Design) wird der Ertrag von zwei Sorten und zwei Stickstoffdüngern miteinander verglichen. Demnach haben wir zwei Behandlungsfaktoren (Sorte & N) mit jeweils zwei Stufen (Sorten A & B, Dünger N1 & N2), sodass es vier Stufenkombinationen gibt (A-N1, A-N2, B-N1 & B-N2). Vor dem Experiment ist natürlich nicht klar wie der Ertrag von den Behandlungen beeinflusst wird. Folgender Plot soll zeigen welche prinzipiellen Effekte die Behandlungen auf den Ertrag haben könnten:
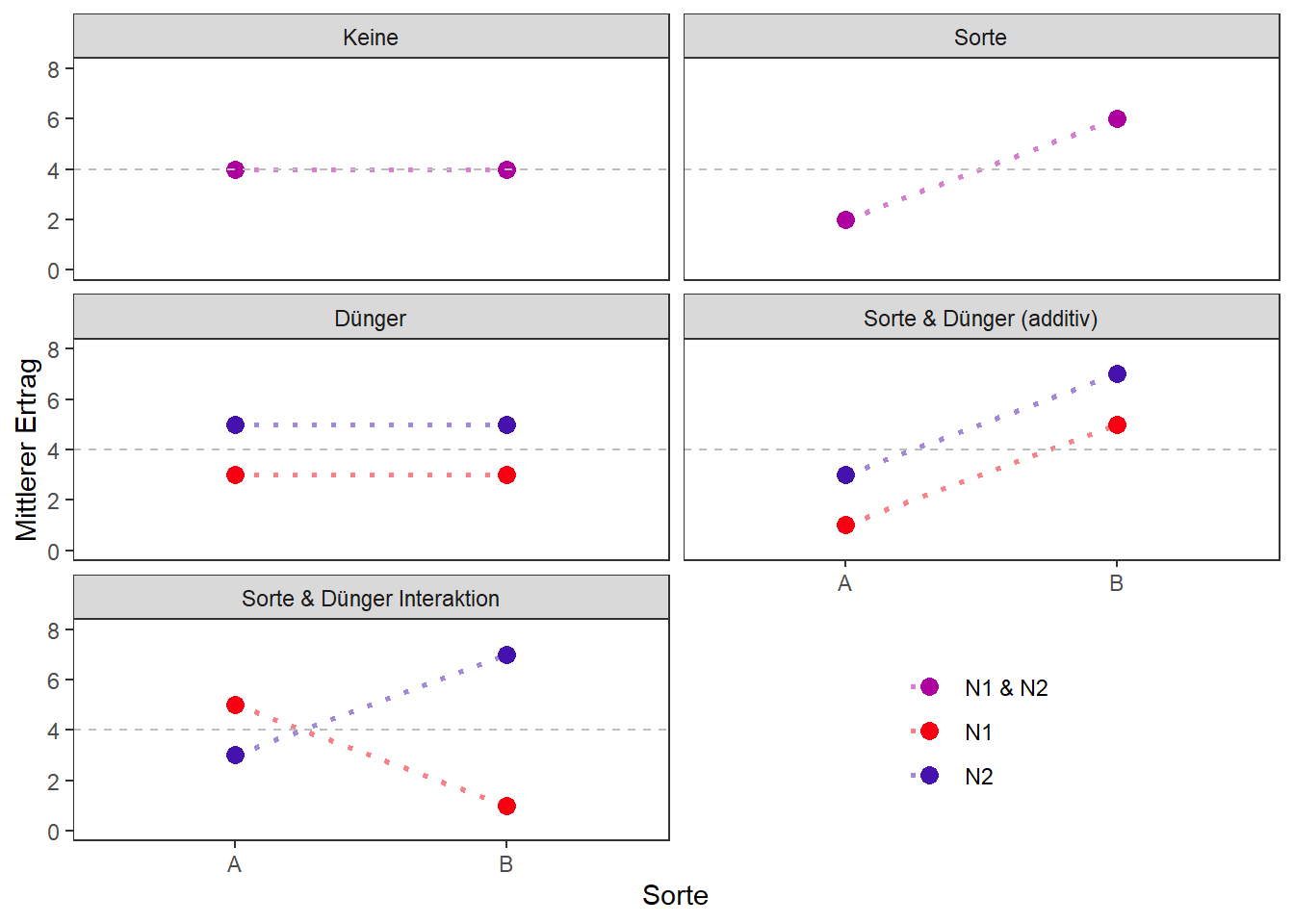
Es muss klar sein, dass natürlich auch die andere Sorte bzw. der andere Stickstoff einen höheren Ertrag zeigen kann - das ist aber nicht Ziel dieses Plots. Was de verschiedenen Plots stattdessen zeigen ist beginnnend von oben links:
- Keine: Alle 4 Stufenkombinationen zeigen gleiche durchschnittliche Erträge. Das bedeutet, dass es weder zwischen den Sorten, noch zwischen den Düngern Unterschiede im Ertrag gibt. Wir finden also weder einen Sorten-, noch einen Düngereffekt. Der Ertrag ist schlichtweg immer 4.
- Sorte: Die durchschnittlichen Erträge der Sorte B sind höher als die der Sorte A. Die Wahl des Düngers macht hierbei keinen Unterschied. Wir finden also einen Sorteneffekt, aber keinen Düngereffekt.
- Dünger: Analog zum vorherigen Punkt können wir natürlich auch umgekehrt herausfinden, dass es einen Düngereffekt, jedoch keinen Sorteneffekt gibt. So zum Beispiel, dass Dünger N2 mehr Ertrag liefert als Dünger N1, die Wahl der Sorte dabei aber keinen Einfluss hat.
- Sorte & Dünger (additiv): In diesem Fall gibt es sowohl einen Sorten-, als auch einen Düngereffekt, die additiv wirken. Das bedeutet, dass z.B. hier Sorte B und Dünger N2 immern den höheren Ertrag liefern, sodass dementsprechend die beste Kombination B-N2 und die schlechteste Kombination A-N1 ist.
- Sorte & Dünger (Interaktion): Schließlich kann es auch sein, dass zwar wieder sowohl die Sorten-, als auch die Düngerwahl zu unterschiedlichen Erträgen führen, dies allerdings nicht rein additiv funktioniert, sondern bestimmte Sorten-Dünger-Kombinationen höhere/niederigere Erträge liefern als erwartet. Das Beispiel im Plot ist dabei ein besonders offensichtlicher Fall, da je nach Dünger eine andere Sorte den höheren Ertrag hat (i.e. die Linien kreuzen sich). Man spricht aber schon dann von einer Interaktion, wenn die Linien nicht parallel sind.
Backward Elimination
Wie gesagt ist vor dem Versuch nicht klar welche Behandlungseffekte es gibt. Um dies herauszufinden kann eine sogenannte backward elimination durchgeführt werden. Bei diesem Verfahren stellt man das volle Modell auf und eliminiert dann Schritt für Schritt die Einflussvariablen. Das volle Modell bezieht sich dabei auf den treatment Teil des Modells. Das bedeutet, dass also noch die design Effekte (z.B. block) des entsprechenden Versuchsdesigns dazukommen. Voll ist das Modell, da man vom untersten Plott, also von Wechselwirkungen der Effekte ausgeht:
- Volles Modell
y = Sorte + Dünger + Sorte:Dünger
Dann führt man eine ANOVA für das volle Modelle durch und betrachtet zuerst den “komplexesten” Term, also hier die Wechselwirkung Sorte:Dünger. Ist diese signifikant, so wird kein Term eliminiert und man hat das finale Modell gefunden. Ist der Term allerdings nicht signifikant, so eliminiert man ihn. Dann passt man im nächsten Schritt das reduzierte Modell an und schaut wieder auf die ANOVA. Dies führt man so lange durch, bis nur noch signifikante treatment Effekte im Modell sind - man eliminiert also alle nicht-signifikanten Effekte aus dem vollen Modell. Je nachdem welche Effekte eliminiert werden, endet man bei einem der Fälle aus dem Plot oben. Wichtig ist wie gesagt, dass man mit dem “komplexesten” Term beginnen muss. Wenn mehrere Terme der gleichen Komplexiztität vorhanden sind, wie bei uns in einem zweiten Schritt Sorte und Dünger, dann wird zuerst der Term mit dem höheren (=weniger signifikanten) p-Wert eliminiert. Hier ist eine Übersicht der Modelle, die den Plots oben entsprechen.
| Plot | Syntax | Formel (für CRD) |
|---|---|---|
| Keine | y = |
\(y_{ijk} = \mu + e_{ijk}\) |
| Sorte | y = Sorte |
\(y_{ijk} = \mu + S_i + e_{ijk}\) |
| Dünger | y = Dünger |
\(y_{ijk} = \mu + D_j + e_{ijk}\) |
| Sorte & Dünger (additiv) | y = Sorte + Dünger |
\(y_{ijk} = \mu + S_i + D_j + e_{ijk}\) |
| Sorte & Dünger (Interaktion) | y = Sorte + Dünger + Sorte:Dünger |
\(y_{ijk} = \mu + S_i + D_j + (SD)_{ij} + e_{ijk}\) |
Mehr als zwei Behandlungsfaktoren
Wenn mehr als zwei Behandlungsfaktoren geprüft werden, gibt es auch mehr als eine potentielle Wechselwirkung:
| Anzahl | Name | Modell |
|---|---|---|
| 2 Faktoren | A & B |
A + B + A:B |
| 3 Faktoren | A, B & C |
A + B + C + A:B + A:C + B:C + A:B:C |
| 4 Faktoren | A, B, C & D |
A + B + C + D + A:B + … + B:C:D + A:B:C:D |
Die backward elimination funktioniert aber genau so wie oben beschrieben. Alternativ zum backward elimination Verfahren kann beispielsweise auch das forward selection Verfahren angewendet werden, bei dem vom leeren Modell ausgegangen wird und Schritt für Schritt ein signifikanter Termin hinzugefügt wird.
Bei Fragen kannst du mir gerne schreiben!
schmidtpaul@hotmail.de